We solve problems

Problems Methods Colouring Colouring (other) Calculus Real numbers Rational and irrational numbers

Ten pairwise distinct non-zero numbers are such that for each two of them either the sum of these numbers or their product is a rational number.

Prove that the squares of all numbers are rational.

Problem #PRU-109881

Problems Calculus Real numbers Integer and fractional parts. Archimedean property Methods Pigeonhole principle Pigeonhole principle (angles and lengths)

13–15 3.0

The polynomial \(P (x)\) of degree \(n\) has \(n\) distinct real roots.

What is the largest number of its coefficients that can be equal to zero?

Problem #PRU-110047

Problems Algebra and arithmetic Rational and irrational numbers

13–15 3.0

We call a number \(x\) rational if it can be represented as \(x=\frac{p}{q}\) for coprime integers \(p\) and \(q\). Otherwise we call the number irrational.
Non-zero numbers \(a\) and \(b\) satisfy the equality \(a^2b^2 (a^2b^2 + 4) = 2(a^6 + b^6)\). Prove that at least one of them is irrational.

Problem #PRU-110122

Problems Algebra and arithmetic Algebraic inequalities and systems of inequalities Algebraic inequalities (other) Calculus Functions of one variable. Continuity Monotonicity, boundedness

14–16 4.0

The functions \(f (x) - x\) and \(f (x^2) - x^6\) are defined for all positive \(x\) and increase. Prove that the function

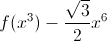
also increases for all positive \(x\).

Problem #PRU-110153

Problems Calculus Real numbers Integer and fractional parts. Archimedean property Methods Pigeonhole principle Pigeonhole principle (angles and lengths)

13–15 3.0

The sum of the positive numbers \(a, b, c\) is \(\pi / 2\). Prove that \(\cos a + \cos b + \cos c > \sin a + \sin b + \sin c\).

Problem #PRU-110157

Problems Geometry Plane geometry Plane transformations Similarity Homothetic transformations, rotations of homothetic transformations Circles Connection between the arc length, the angle, and the chord Calculus Derivative Derivative and multiple roots

14–16 5.0

The circles \(\sigma_1\) and \(\sigma_2\) intersect at points \(A\) and \(B\). At the point \(A\) to \(\sigma_1\) and \(\sigma_2\), respectively, the tangents \(l_1\) and \(l_2\) are drawn. The points \(T_1\) and \(T_2\) are chosen respectively on the circles \(\sigma_1\) and \(\sigma_2\) so that the angular measures of the arcs \(T_1A\) and \(AT_2\) are equal (the arc value of the circle is considered in the clockwise direction). The tangent \(t_1\) at the point \(T_1\) to the circle \(\sigma_1\) intersects \(l_2\) at the point \(M_1\). Similarly, the tangent \(t_2\) at the point \(T_2\) to the circle \(\sigma_2\) intersects \(l_1\) at the point \(M_2\). Prove that the midpoints of the segments \(M_1M_2\) are on the same line, independent of the positions of the points \(T_1, T_2\).

Problem #PRU-110210

Problems Calculus Real numbers Integer and fractional parts. Archimedean property Methods Pigeonhole principle Pigeonhole principle (angles and lengths)

13–15 3.0

Prove that for each \(x\) such that \(\sin x \neq 0\), there is a positive integer \(n\) such that \(|\sin nx| \geq \sqrt{3}/2\).

Problem #PRU-110212

Problems Calculus Real numbers Integer and fractional parts. Archimedean property Methods Pigeonhole principle Pigeonhole principle (angles and lengths)

13–15 3.0

For what natural numbers \(n\) are there positive rational but not whole numbers \(a\) and \(b\), such that both \(a + b\) and \(a^n + b^n\) are integers?

Problem #PRU-111218

Problems Calculus Real numbers Integer and fractional parts. Archimedean property Methods Pigeonhole principle Pigeonhole principle (angles and lengths)

13–15 3.0

The base of the pyramid is a square. The height of the pyramid crosses the diagonal of the base. Find the largest volume of such a pyramid if the perimeter of the diagonal section containing the height of the pyramid is 5.

Problem #PRU-111415

Problems Calculus Real numbers Integer and fractional parts. Archimedean property Methods Pigeonhole principle Pigeonhole principle (angles and lengths)

13–15 3.0

The volume of the regular quadrangular pyramid \(SABCD\) is equal to \(V\). The height \(SP\) of the pyramid is the edge of the regular tetrahedron \(SPQR\), the plane of the face \(PQR\) which is perpendicular to the edge \(SC\). Find the volume of the common part of these pyramids.