Problems
Given a square trinomial \(f (x) = x^2 + ax + b\). It is known that for any real \(x\) there exists a real number \(y\) such that \(f (y) = f (x) + y\). Find the greatest possible value of \(a\).
In the infinite sequence \((x_n)\), the first term \(x_1\) is a rational number greater than 1, and \(x_{n + 1} = x_n + \frac{1}{\lfloor x_n\rfloor }\) for all positive integers \(n\).
Prove that there is an integer in this sequence.
Note that in this problem, square brackets represent integers and curly brackets represent non-integer values or 0.
On the plane coordinate axes with the same but not stated scale and the graph of the function \(y = \sin x\), \(x\) \((0; \alpha)\) are given.
How can you construct a tangent to this graph at a given point using a compass and a ruler if: a) \(\alpha \in (\pi /2; \pi)\); b) \(\alpha \in (0; \pi /2)\)?
The sequence \(a_1, a_2, \dots\) is such that \(a_1 \in (1,2)\) and \(a_{k + 1} = a_k + \frac{k}{a_k}\) for any positive integer \(k\). Prove that it cannot contain more than one pair of terms with an integer sum.The sequence \(a_1, a_2, \dots\) is such that \(a_1 \in (1,2)\) and \(a_{k + 1} = a_k + \frac{k}{a_k}\) for any positive integer \(k\). Prove that it cannot contain more than one pair of terms with an integer sum.
Prove that if the expression
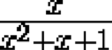
takes a rational value, then the expression
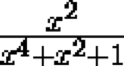
also takes on a rational value.
Prove that if the numbers \(x, y, z\) satisfy the following system of equations for some values of \(p\) and \(q\): \[\begin{aligned} y &= x^2 + px + q,\\ z &= y^2 + py + q,\\ x &= z^2 + pz + q, \end{aligned}\] then the inequality \(x^2y + y^2z + z^2x \geq x^2z + y^2x + z^2y\) is satisfied.
The nonzero numbers \(a\), \(b\), \(c\) are such that every two of the three equations \(ax^{11} + bx^4 + c = 0\), \(bx^{11} + cx^4 + a = 0\), \(cx^{11} + ax^4 + b = 0\) have a common root. Prove that all three equations have a common root.
The teacher wrote on the board in alphabetical order all possible \(2^n\) words consisting of \(n\) letters A or B. Then he replaced each word with a product of \(n\) factors, correcting each letter A by \(x\), and each letter B by \((1 - x)\), and added several of the first of these polynomials in \(x\). Prove that the resulting polynomial is either a constant or increasing function in \(x\) on the interval \([0, 1]\).
We are given a polynomial \(P(x)\) and numbers \(a_1\), \(a_2\), \(a_3\), \(b_1\), \(b_2\), \(b_3\) such that \(a_1a_2a_3 \ne 0\). It turned out that \(P (a_1x + b_1) + P (a_2x + b_2) = P (a_3x + b_3)\) for any real \(x\). Prove that \(P (x)\) has at least one real root.
There is a group of 5 people: Alex, Beatrice, Victor, Gregory and Deborah. Each of them has one of the following codenames: V, W, X, Y, Z. We know that:
Alex is 1 year older than V,
Beatrice is 2 years older than W,
Victor is 3 years older than X,
Gregory is 4 years older than Y.
Who is older and by how much: Deborah or Z?