Problems

A monkey becomes happy when they eat three different fruits. What is the largest number of monkeys that can become happy with \(20\) pears, \(30\) bananas, \(40\) peaches and \(50\) tangerines?

On a \(10\times 10\) board, a bacterium sits in one of the cells. In one move, the bacterium shifts to a cell adjacent to the side (i.e. not diagonal) and divides into two bacteria (both remain in the same new cell). Then, again, one of the bacteria sitting on the board shifts to a new adjacent cell, either horizontally or vertically, and divides into two, and so on. Is it possible for there to be an equal number of bacteria in all cells after several such moves?

One cell was cut out of a \(3\times6\) rectangle, as seen in the diagram. How should you glue this cell in a different place to get a figure that can be cut into two identical ones? If needed, the resulting parts can be rotated and reflected.

In the sum below, different letters denote different digits and the same letters denote the same digit. \[P.Z + T.C + D.R + O.B + E.Y\] None of the five terms are integers, but the sum itself is an integer. Find the possible sums of the expression. For each possible answer, write one example with these five terms. Explain why other sums cannot be obtained.

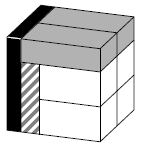
Michael made a cube with edge \(1\) out of eight bars as in the picture. All \(8\) bars have the same volume. The dimensions of the grey bars are the same as each other. Similarly, the dimensions of the white bars are the same as each other. Find the lengths of the edges of the white bars.

Peter went to the Museum of Modern Art and saw a square painting in a frame of an unusual shape. The frame consisted of \(21\) congruent triangles. Peter was interested in what the angles of these triangles were equal to. Help him find these angles.

Red, blue and green chameleons live on an island. One day \(35\) chameleons stood in a circle. A minute later, they all changed colour at the same time, each changing into the colour of one of their neighbours. A minute later, everyone again changed their colours at the same time into the colour of one of their neighbours. Is it ever possible that each chameleon was each of the colours red, blue and green at some point? For example, it’s allowed for a chameleon to start off blue, turn green after one minute, then turn red after the second minute. It’s not allowed for a chameleon to start off blue, turn green after one minute, but then turn back to blue after the second minute.

Let \(p\) and \(q\) be two prime numbers such that \(q = p + 2\). Prove that \(p^q + q^p\) is divisible by \(p + q\).

For any real number \(x\), the absolute value of \(x\), written \(\left| x \right|\), is defined to be \(x\) if \(x>0\) and \(-x\) if \(x \leq 0\). What are \(\left| 3 \right|\), \(\left| -4.3 \right|\) and \(\left| 0 \right|\)?

Let \(x\) and \(y\) be real numbers. Prove that \(x \leq \left| x \right|\) and \(0 \leq \left| x \right|\). Then prove that the following inequality holds \(\left| x+y \right| \leq \left| x \right|+\left| y \right|\).

There are \(n\) balls labelled 1 to \(n\). If there are \(m\) boxes labelled 1 to \(m\) containing the \(n\) balls, a legal position is one in which the box containing the ball \(i\) has number at most the number on the box containing the ball \(i+1\), for every \(i\).

There are two types of legal moves: 1. Add a new empty box labelled \(m+1\) and pick a box from box 1 to \(m+1\), say the box \(j\). Move the balls in each box with (box) number at least \(j\) up by one box. 2. Pick a box \(j\), shift the balls in the boxes with (box) number strictly greater than \(j\) down by one box. Then remove the now empty box \(m\).

Prove it is possible to go from an initial position with \(n\) boxes with the ball \(i\) in the box \(i\) to any legal position with \(m\) boxes within \(n+m\) legal moves.