Problems
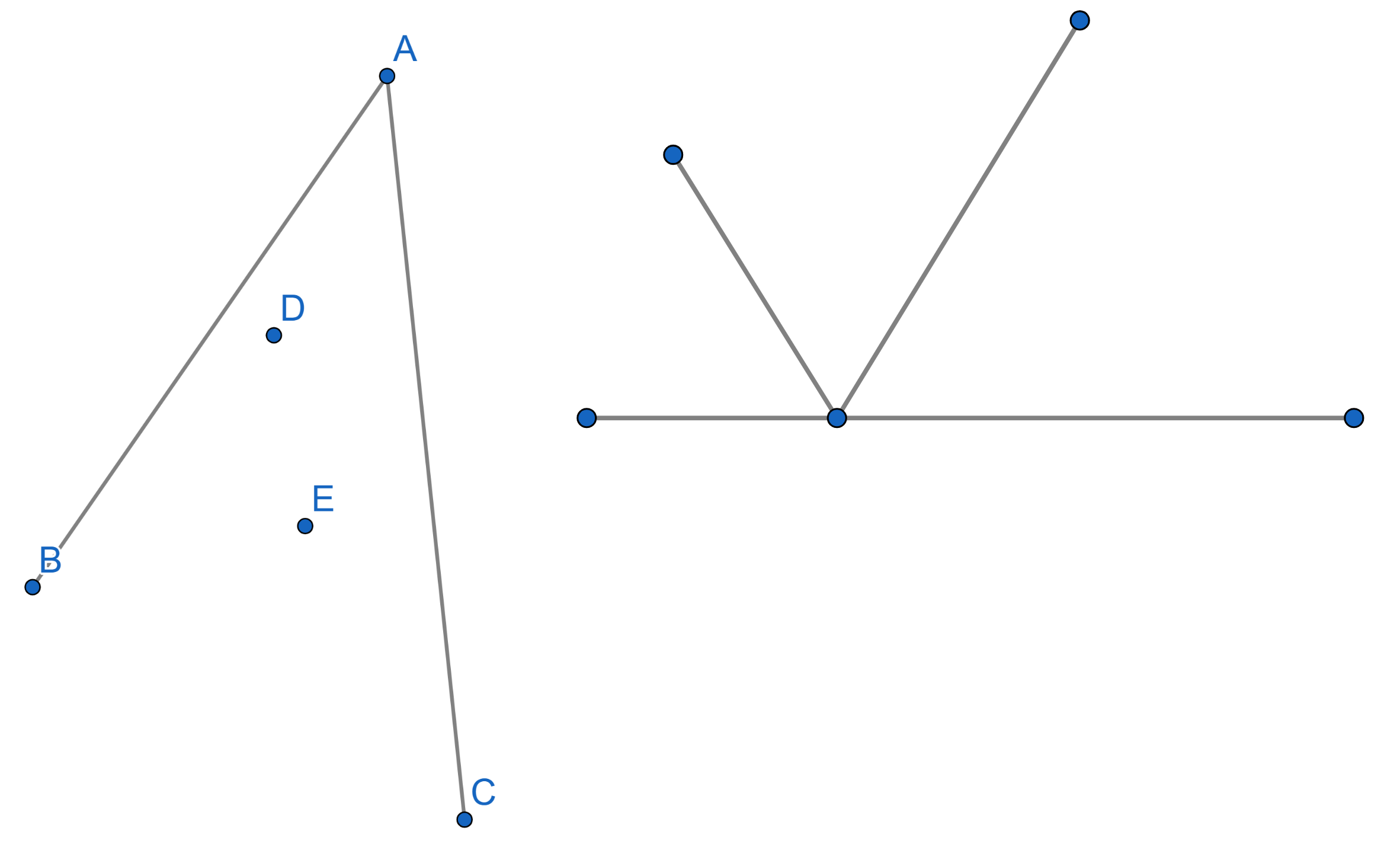
Between two mirrors \(AB\) and \(AC\), forming a sharp angle two points
\(D\) and \(E\) are located. In what direction should
one shine a ray of light from the point \(D\) in such a way that it would reflect off
both mirrors and hit the point \(E\)?
If a ray of light comes towards a surface under a certain angle, it is
reflected with the same angle as on the picture.
Consider a set of natural numbers \(A\), consisting of all numbers divisible by \(6\), let \(B\) be the set of all natural numbers divisible by \(8\), and \(C\) be the set of all natural numbers divisible by \(12\). Describe the sets \(A\cup B\), \(A\cup B\cup C\), \(A\cap B\cap C\), \(A-(B\cap C)\).
Prove that the set of all finite subsets of natural numbers \(\mathbb{N}\) is countable. Then prove that the set of all subsets of natural numbers is not countable.
Most magic tricks rely on some kind of sleight of hand. However, some tricks are powered by maths!
A fruitful way of analyzing card shuffles is by using the idea of “permutations". Permutations are important objects that occur in various parts of maths. Many interesting patterns emerge, and we will only touch the tip of the iceberg today.
Suppose you have a set of ordered objects. A permutation of this set is a reordering of the objects. For example, a permutation of a deck of cards ordered from top to bottom is simply a shuffle of the cards. Note that in general, a permutation can be defined as a relabelling of objects, so an order is not necessary.
Let’s discuss two ways of writing permutations.
The first way is two-line notation. Say you have the cards from top to bottom Ace, two, three. Say Ace is 1. Suppose that after a shuffle \(p\), we have from top to bottom two, three, Ace. The two-line notation keeps the original positions on the first line and the new positions in the second line.
\[p = \left( \begin{array}{ccc} 1 & 2 & 3 \\ 3 & 1 & 2 \\ \end{array} \right).\]
A second way of writing permutations is function notation. In the same situation, we could write \(p(1)=3\), \(p(2)=1\) and \(p(3)=2\).
As a first indication of why permutations give a useful perspective, we note that permutations can be done after another and the result is still a permutation. Let \(q\) be the permutation on the same three cards given by \(q(1)=2\), \(q(2)=3\) and \(q(3)=1\). Consider \(qp\) which is performing \(p\) first and then \(q\). To find out what the effect of this composite permutation is on \(1\), we can visualize it as follows: \[1\mapsto3=p(1)\mapsto q(p(1))=q(3)=1.\]
This shows that the function notation plays very nicely with composing permutations. By the way, if we work out the entire \(qp\) in this fashion, we find that \[qp = \left( \begin{array}{ccc} 1 & 2 & 3 \\ 1 & 2 & 3 \\ \end{array} \right).\]
In other words, \(q\) has “negated" the effect of \(p\)!
We often think of symmetry as a property of shapes. Another way of thinking about it is as something you do to an object which keeps the object looking the same. The example you’ve likely met is reflection. The other one that we’ll consider today is rotation. An important feature is that we consider ‘doing nothing’ as a symmetry - we call this the identity.
An equation of the form \(x^2 - dy^2 = 1\) where \(d>0\) is a nonsquare (what if \(d\) is a square?) integer and we seek \(x,y\) in the integers is called Pell’s equation. By changing the sign of \(x\) and \(y\), we may assume they are nonnegative. There is always the solution \((x,y)=(1,0)\) which we call trivial.
Here is a useful way to think about the solutions to Pell’s equations. The difference of squares identity prompts us to consider the solution \((x,y)\) to Pell’s equation as the real number \(x+y\sqrt{d}\). The fact that \((x,y)\) is a solution simply means \((x+y\sqrt{d})(x-y\sqrt{d})=1\).
Here is some common notation you might see if you look at books or on the internet: if we have a number \(u=x+y\sqrt{d}\), we can define its conjugate as the number \(\bar u=x-y\sqrt{d}\). Moreover, the set of numbers of the form \(x+y\sqrt{d}\) where \(x,y\) are whole numbers, is often written as \(\mathbb Z[\sqrt{d}]\) (pronounced “integers adjoint \(\sqrt{d}\)"). Therefore, a number \(u\) that belongs to \(\mathbb Z[\sqrt{d}]\) is a solution to Pell’s equation if \(u\bar u=1\).
As with all Diophantine equations, we would like to to know the following about Pell’s equation.
Does Pell’s equation always have nontrivial solutions?
When Pell’s equation does have solutions, is the number of solutions finite?
How can we describe all solutions to Pell’s equation?
In this sheet, we answer all of the questions above and apply these theoretical results to some other problems.
Remainder is the number that is “left over" from division. Even if a number is not divisible by another number fully, we can still divide, but leaving a remainder. The remainder is less than the number we’re dividing by. For example, a remainder of \(44\) in division by \(7\) is \(2\), because \(44 = 6 \times 7 + 2\). More generally, we can write \(n=qk+r\), where \(0\leq r<k\). We say that \(k\) goes into \(n\) \(q\) times, and a little bit (\(r\)) is left. If that little bit was larger than \(k\), it could “go into" \(n\) once more.
The general rule is that a remainder of a sum, difference or a product of two remainders is equal to the remainder of a sum, difference or a product of the original numbers. What that means is if we want to find a remainder of a product of two numbers, we need to look at the individual remainders, multiply them, and then take a remainder.
For example, \(10\) has remainder \(3\) when dividing by \(7\) and \(11\) has remainder \(4\) when dividing by \(7\). The product \(10\times11=110\) will have the same remainder as the product of the individual remainders. We first multiply \(3\times4=12\) and then take a remainder upon division by \(7\), which is \(5\) because \(12=7+5\). That means that \(110\) gives a remainder \(5\) in division by \(7\) - and it does, because \(110=15\times7+5\). If a number is divisible by a number we are dividing it, nothing remains and we say the remainder is \(0\).
Let’s have a look on some examples:
Let us define XOR (or addition mod 2). XOR is defined for 0 and 1 only. Here is a table recording the values of XOR:
| XOR | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 0 |
Now we define the important concept of nim-sum. Given two natural numbers \(x\) and \(y\), we first convert them into binary representations and then compute XOR on individual digits. The resulting number, denoted \(x \oplus y\), is the nim-sum of \(x\) and \(y\). Here is an example.
| 1 | 0 | 1 | 1 | 0 | |
| XOR | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 |
This is simply saying \(22 \oplus 5 = 19\). Note that \(22=(10110)_2\) and \(5=(00101)_2\).
Verify \((x \oplus y) \oplus z = x \oplus (y \oplus z)\), so we can speak of \(x \oplus y \oplus z\) with no ambiguity.
Show that \(x \oplus y = 0\) if and only if \(x = y\). Remember that \(x \oplus y\) denotes the nim-sum of \(x\) and \(y\).
Show that \(\text{Nim}(x,y,z)\) is a losing position if and only if \(x \oplus y \oplus z = 0\). Remember that \(x \oplus y\) denotes the nim-sum of \(x\) and \(y\).