Problems
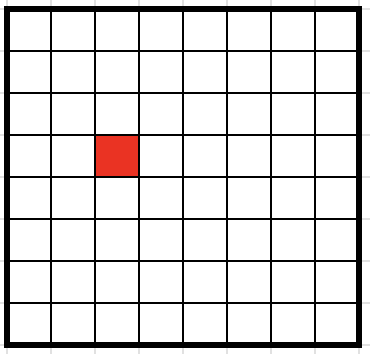
One square is coloured red at random on an \(8\times8\) grid. Show that no matter where this red square is, you can cover the remaining \(63\) squares with \(21\) ‘L’ triominoes, with no gaps or overlaps.

Let \(n\) be a positive integer. Show that \(1+3+3^2+...+3^{n-1}+3^n=\frac{3^{n+1}-1}{2}\).
Show that all integers greater than or equal to \(8\) can be written as a sum of some \(3\)s and \(5\)s. e.g. \(11=3+3+5\). Note that there’s no way to write \(7\) in such a way.
Find a formula for \(R(2,k)\), where \(k\) is a natural number.
Show that \(R(4,3)\ge9\). That is, there exists a way of colouring the edges of \(K_8\) with no red \(K_4\), nor any blue \(K_3\).
Show that \(R(4,4)\ge18\) - that is, there’s a way of colouring the edges of \(K_{17}\) such that there’s no monochromatic \(K_4\).
Show that \(R(4,3)\le9\). That is, no matter how you colour the edge of \(K_9\), there must be a red \(K_4\) or a blue \(K_3\).
Show that \(R(4,4)\le18\) - that is, no matter how you colour the edges of \(K_{18}\), there must be a monochromatic \(K_4\).
By considering \(k-1\) copies of \(K_{k-1}\), show that \(R(k,k)\ge(k-1)^2\).