Problems
Every year the citizens of the planet “Lotsofteeth" enter a contest
to see who has the most teeth.
This year the judge notices:
Nobody has 0 teeth (everyone has at least 1).
There are more people in the contest than the most teeth that any one person has. (For example, if the most teeth anyone has is 27, then there are more than 27 people participating in the contest.)
Must there be two people who have exactly the same number of teeth? Explain why.
Long before meeting Snow White, the seven dwarves lived in seven different mines. There is an underground tunnel connecting any two mines. All tunnels were separate, so you could not start in one tunnel and somehow end up in another. Is it possible to walk through every tunnel exactly once without retracing your path?
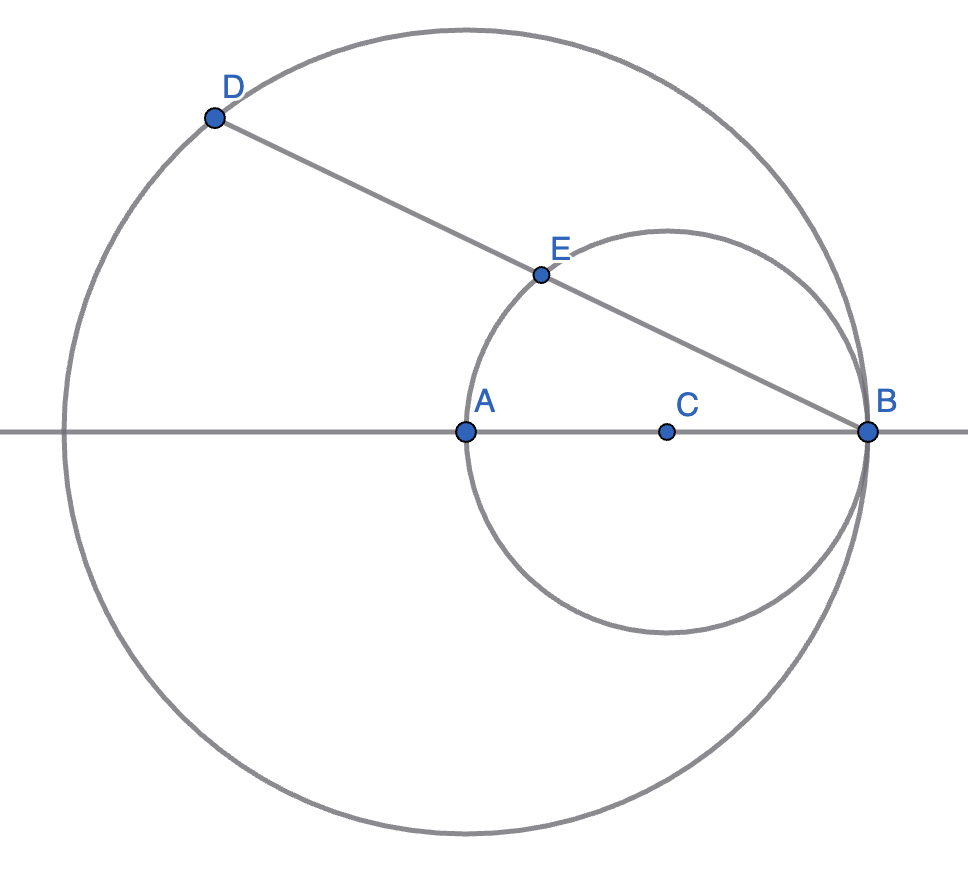
A circle with centre \(A\) has the point \(B\) on its circumference. A smaller circle is drawn inside this with \(AB\) as a diameter and \(C\) as its centre. A point \(D\) (which is not \(B\)) is chosen on the circumference of the bigger circle, and the line \(BD\) is drawn. \(E\) is the point where the line \(BD\) intersects the smaller circle.
Show that \(|BE|=|DE|\).
A circle with center \(A\) is inscribed into a square \(CDFE\). A line \(GH\) intersects the sides \(CD\) and \(CE\) of the square and is tangent to the circle at the point \(I\). Find the perimeter of the triangle \(CHG\) (the sum of lengths of all the sides) if the side of the square is \(10\)cm.

Let \(x,x',y,y'\) be integers such that \(x+\sqrt{d}y=x'+\sqrt{d}y'\), where \(d\) is a number that is not a square. Show that \(x=x'\) and \(y=y'\).
Show that if \(u_1\) and \(u_2\) are solutions to Pell’s equation, then \(u_1u_2\) is also a solution to Pell’s equation. What can you conclude about the number of solutions, if there are any?
Find all integer solutions to \(x^2+y^2-1=4xy\).
In a bag we have \(99\) red balls and \(99\) blue balls. We take balls from the bag, two balls at a time:
If the two balls are of the same colour, then we put in a red ball to the bag.
If the two balls are of different colour, we return a blue ball to the bag.
Regardless, after each step, one ball is lost from the bag, so eventually there will be only one ball. What is the colour of this last ball?
You have an \(8\times 8\) chessboard coloured in the usual way. You can pick any \(2\times 1\) or \(1\times 2\) piece and flip the white tiles to black tiles and vice-versa. Is it possible to finish with \(63\) white pieces and \(1\) black piece?
We start with the point \(S=(1,3)\) of the plane. We generate a sequence of points with coordinates \((x_n,y_n)\) with the following rule: \[x_0=1,y_0=3\qquad x_{n+1}=\frac{x_n+y_n}{2}\qquad y_{n+1}=\frac{2x_ny_n}{x_n+y_n}\] Is the point \((3,2)\) in the sequence?