Problems

Does there exist a function \(f (x)\) defined for all \(x \in \mathbb{R}\) and for all \(x, y \in \mathbb{R}\) satisfying the inequality \(| f (x + y) + \sin x + \sin y | < 2\)?

The real numbers \(x\) and \(y\) are such that for any distinct prime odd \(p\) and \(q\) the number \(x^p + y^q\) is rational. Prove that \(x\) and \(y\) are rational numbers.

The functions \(f (x) - x\) and \(f (x^2) - x^6\) are defined for all positive \(x\) and increase. Prove that the function

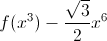
also increases for all positive \(x\).

The circles \(\sigma_1\) and \(\sigma_2\) intersect at points \(A\) and \(B\). At the point \(A\) to \(\sigma_1\) and \(\sigma_2\), respectively, the tangents \(l_1\) and \(l_2\) are drawn. The points \(T_1\) and \(T_2\) are chosen respectively on the circles \(\sigma_1\) and \(\sigma_2\) so that the angular measures of the arcs \(T_1A\) and \(AT_2\) are equal (the arc value of the circle is considered in the clockwise direction). The tangent \(t_1\) at the point \(T_1\) to the circle \(\sigma_1\) intersects \(l_2\) at the point \(M_1\). Similarly, the tangent \(t_2\) at the point \(T_2\) to the circle \(\sigma_2\) intersects \(l_1\) at the point \(M_2\). Prove that the midpoints of the segments \(M_1M_2\) are on the same line, independent of the positions of the points \(T_1, T_2\).

A continuous function \(f(x)\) is such that for all real \(x\) the following inequality holds: \(f(x^2) - (f (x))^2 \geq 1/4\). Is it true that the function \(f(x)\) necessarily has an extreme point?

The quadratic trinomials \(f (x)\) and \(g (x)\) are such that \(f' (x) g' (x) \geq | f (x) | + | g (x) |\) for all real \(x\). Prove that the product \(f (x) g (x)\) is equal to the square of some trinomial.

Given a square trinomial \(f (x) = x^2 + ax + b\). It is known that for any real \(x\) there exists a real number \(y\) such that \(f (y) = f (x) + y\). Find the greatest possible value of \(a\).

Prove that if the numbers \(x, y, z\) satisfy the following system of equations for some values of \(p\) and \(q\): \[\begin{aligned} y &= x^2 + px + q,\\ z &= y^2 + py + q,\\ x &= z^2 + pz + q, \end{aligned}\] then the inequality \(x^2y + y^2z + z^2x \geq x^2z + y^2x + z^2y\) is satisfied.

We are given a polynomial \(P(x)\) and numbers \(a_1\), \(a_2\), \(a_3\), \(b_1\), \(b_2\), \(b_3\) such that \(a_1a_2a_3 \ne 0\). It turned out that \(P (a_1x + b_1) + P (a_2x + b_2) = P (a_3x + b_3)\) for any real \(x\). Prove that \(P (x)\) has at least one real root.

It is known that a certain polynomial at rational points takes rational values. Prove that all its coefficients are rational.