Problems

Is it possible to cover a \((4n+2) \times (4n+2)\) board with the \(L\)-tetraminos without overlapping for any \(n\)? The pieces can be flipped and turned.

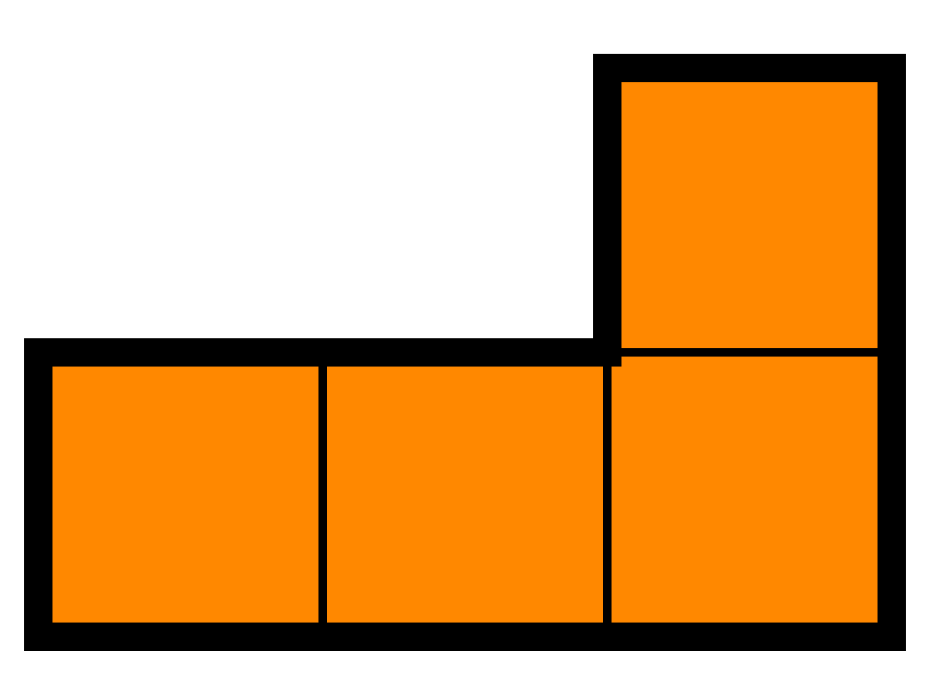
Is it possible to cover a \(4n \times 4n\) board with the \(L\)-tetraminos without overlapping for any \(n\)? The pieces can be flipped and turned.

Definition A set is a collection of elements, containing only one copy of each element. The elements are not ordered, nor they are governed by any rule. We consider an empty set as a set too.
There is a set \(C\) consisting of \(n\) elements. How many sets can be constructed using the elements of \(C\)?

Given a natural number \(n\) you are allowed to perform two operations: "double up", namely get \(2n\) from \(n\), and "increase by \(1\)", i.e. to get \(n+1\) from \(n\). Find the smallest amount of operations one needs to perform to get the number \(n\) from \(1\).

There are \(100\) people standing in line, and one of them is Arthur. Everyone in the line is either a knight, who always tells the truth, or a liar who always lies. Everyone except Arthur said, "There are exactly two liars between Arthur and me." How many liars are there in this line, if it is known that Arthur is a knight?

A rectangular parallelepiped of the size \(m\times n\times k\) is divided into unit cubes. How many rectangular parallelepipeds are formed in total (including the original one)?

In the Land of Linguists live \(m\) people, who have opportunity to speak \(n\) languages. Each person knows exactly three languages, and the sets of known languages may be different for different people. It is known that \(k\) is the maximum number of people, any two of whom can talk without interpreters. It turned out that \(11n \leq k \leq m/2\). Prove that then there are at least \(mn\) pairs of people in the country who will not be able to talk without interpreters.

Detective Nero Wolf investigates a crime. He’s got \(80\) people involved in the case, among whom one is a criminal and another is a witness to the crime (but it is not known who either of them are). Each day the detective may invite one or more of these \(80\) people, and if there is a witness among those invited, but not the perpetrator, the witness will report who the perpetrator is. Can the detective solve a case in \(12\) days?

The king decided to reward a group of \(n\) wise men. They will be placed in a row one after the other (so that everyone is looking in the same direction), and each is going to wear a black or a white hat. Everyone will see the hats of everyone in front, but not those behind them. The wise men will take turns (from the last to the first) to name the color (white or black) and the natural number of their choice.
At the end, the number of sages who have named the color of their hat correctly is counted: that is exactly how many days the whole group will be paid a salary raise. The wise men were allowed to agree in advance on how to respond. At the same time, the wise men know that exactly \(k\) of them are insane (they do not know who exactly). Any insane man names the color white or black, regardless of the agreement. What is the maximum number of days with a pay supplement that the wise men can guarantee to a group, regardless of the location of the insane in the queue?

A whole number of litres of water were poured into three vessels. You can only to pour into any vessel the exact amount of water equal to the amount it already contains from any other vessel. Prove that in a few transfusions one can empty one of the vessels. The vessels are large enough: each can hold all the water.