Problems

A coin is tossed three times. How many different sequences of heads and tails can you get?

Two expressions are written on the board:

$$1+22+333+4444+55555+666666+7777777+88888888+999999999$$ $$9+98+987+9876+98765+987654+9876543+98765432+987654321$$

Determine which one is greater or whether the numbers are equal.

Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a square, or slightly harder in a shape of a given rectangle.

Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a given triangle.

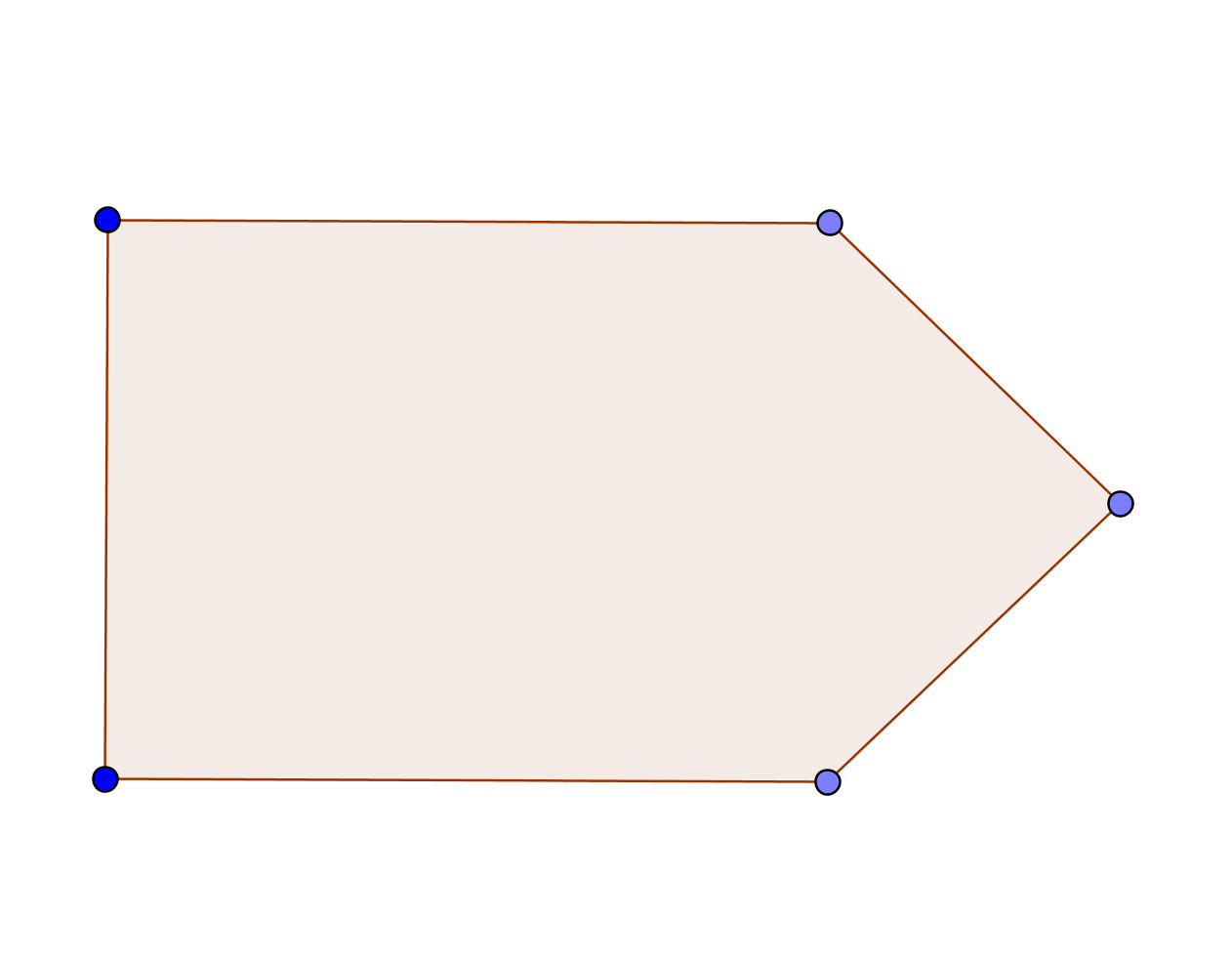
Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a shape like this

Draw a picture how Robinson used to tie the goat and the wolf in order for the goat to graze the grass in the shape of half a circle.

Let $r$ be a rational number and $x$ be an irrational number (i.e. not a rational one). Prove that the number $r+x$ is irrational.
If $r$ and $s$ are both irrational, then must $r+s$ be irrational as well?

Definition: We call a number $x$ rational if there exist two integers $p$ and $q$ such that $x=\frac{p}{q}$. We assume that $p$ and $q$ are coprime.
Prove that $\sqrt{2}$ is not rational.

Let $n$ be an integer such that $n^2$ is divisible by $2$. Prove that $n$ is divisible by $2$.

Let $n$ be an integer. Prove that if $n^3$ is divisible by $3$, then $n$ is divisible by $3$.