Problems

Paloma wrote digits from \(0\) to \(9\) in each of the \(9\) dots below, using each digit at most once. Since there are \(9\) dots and \(10\) digits, she must have missed one digit.

In the triangles, Paloma started writing either the three digits at the corners added together (the sum), or the three digits at the corners multiplied together (the product). She gave up before finishing the final two triangles.

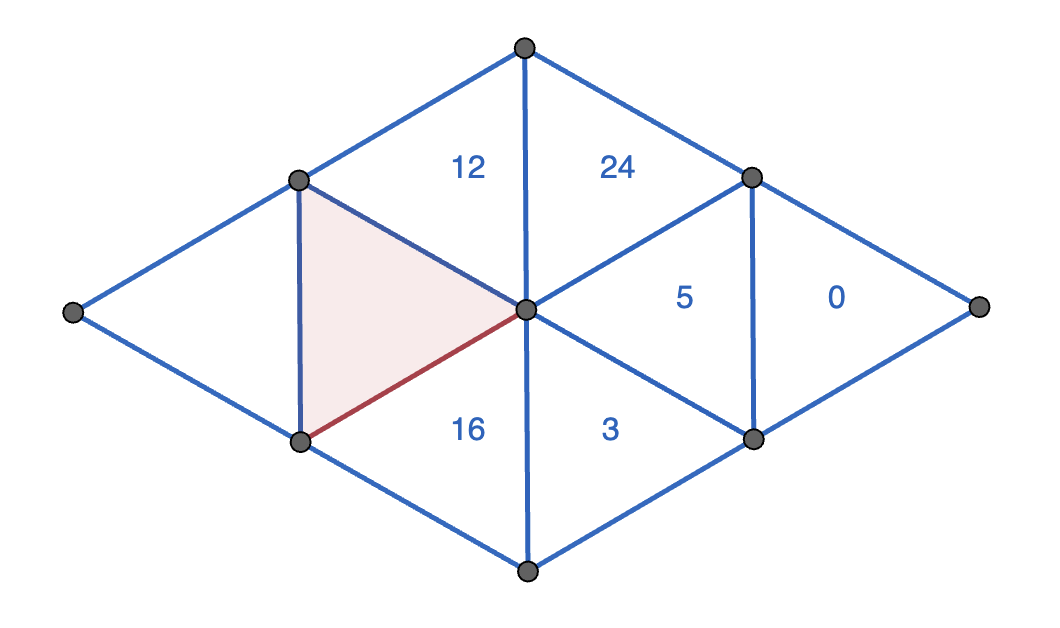
What numbers could Paloma have written in the interior of the red triangle? Demonstrate that you’ve found all of the possibilities.

How many subsets are there of \(\{1,2,...,10\}\) (the integers from \(1\) to \(10\) inclusive) containing no consecutive digits? That is, we do count \(\{1,3,6,8\}\) but do not count \(\{1,3,6,7\}\).
For example, when \(n=3\), we have \(8\) subsets overall but only \(5\) contain no consecutive integers. The \(8\) subsets are \(\varnothing\) (the empty set), \(\{1\}\), \(\{2\}\), \(\{3\}\), \(\{1,3\}\), \(\{1,2\}\), \(\{2,3\}\) and \(\{1,2,3\}\), but we exclude the final three of these.

For any positive integer \(k\), the factorial \(k!\) is defined as a product of all integers between 1 and \(k\) inclusive: \(k! = k \times (k-1) \times ... \times 1\). What’s the remainder when \(2025!+2024!+2023!+...+3!+2!+1!\) is divided by \(8\)?

Let \(u\) and \(v\) be two positive integers, with \(u>v\). Prove that a triangle with side lengths \(u^2-v^2\), \(2uv\) and \(u^2+v^2\) is right-angled.

We call a triple of natural numbers (also known as positive integers) \((a,b,c)\) satisfying \(a^2+b^2=c^2\) a Pythagorean triple. If, further, \(a\), \(b\) and \(c\) are relatively prime, then we say that \((a,b,c)\) is a primitive Pythagorean triple.

Show that every primitive Pythagorean triple can be written in the form \((u^2-v^2,2uv,u^2+v^2)\) for some coprime positive integers \(u>v\).

The lengths of three sides of a right-angled triangle are all integers.

Show that one of them is divisible by \(5\).

There are two imposters and seven crewmates on the rocket ‘Plus’. How many ways are there for the nine people to split into three groups of three, such that each group has at least two crewmates? The two imposters and seven crewmates are all distinguishable from each other, but we’re not concerned with the order of the three groups.

For example: \(\{I_1,C_1,C_2\}\), \(\{I_2,C_3,C_4\}\) and \(\{C_5,C_6,C_7\}\) is the same as \(\{C_3,C_4,I_2\}\), \(\{C_5,C_6,C_7\}\) and \(\{I_1,C_2,C_1\}\) but different from \(\{I_2,C_1,C_2\}\), \(\{I_1,C_3,C_4\}\) and \(\{C_5,C_6,C_7\}\).

Draw the plane tiling with regular hexagons.

Can you tile the plane with regular octagons?

Draw how to tile the whole plane with figures, composed from squares \(1\times 1\), \(2\times 2\), \(3\times 3\), \(4\times 4\), and \(5\times 5\) where squares of all sizes are used the same amount of times in the design of the figure.