Problems

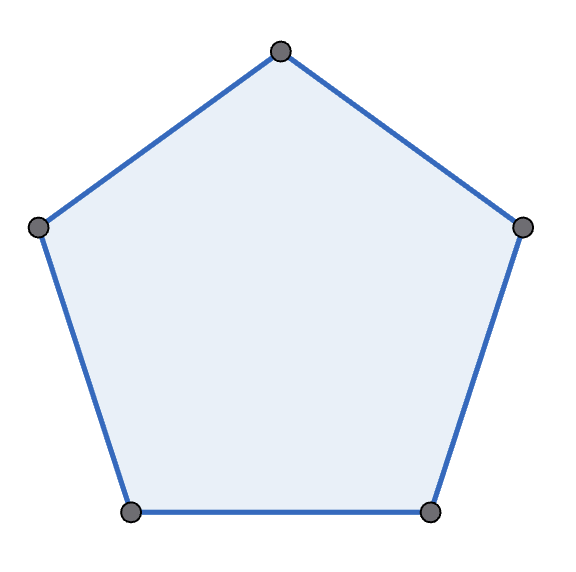
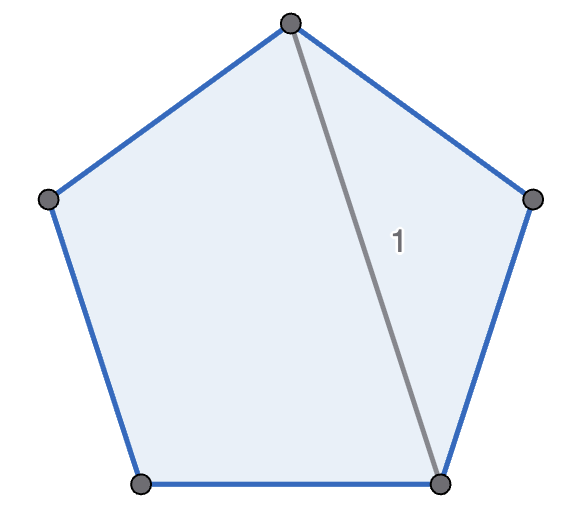
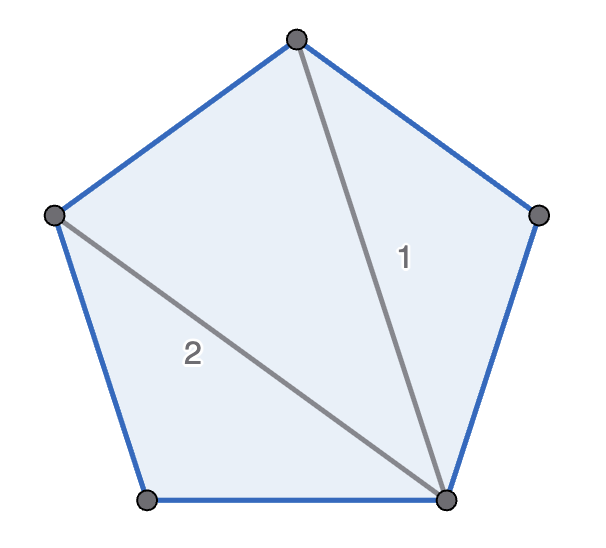
Michelle and Mondo play the following game, with Michelle going first. They start with a regular polygon, and take it in turns to move. A move is to pick two non-adjacent points in one polygon, connect them, and split that polygon into two new polygons. A player wins if their opponent cannot move - which happens if there are only triangles left. See the diagram below for an example game with a pentagon. Prove that Michelle has the winning strategy if they start with a decagon (\(10\)-sided polygon).

Let \(n\) be a positive integer. Show that \(1+3+3^2+...+3^{n-1}+3^n=\frac{3^{n+1}-1}{2}\).

Show that all integers greater than or equal to \(8\) can be written as a sum of some \(3\)s and \(5\)s. e.g. \(11=3+3+5\). Note that there’s no way to write \(7\) in such a way.

Let \(\phi(n)\) be Euler’s function. Namely \(\phi(n)\) counts how many integers from \(1\) to \(n\) inclusive are coprime with \(n\). For two natural numbers \(m\), \(n\) such that \(\gcd(m,n)=1\), prove that \(\phi(mn) = \phi(m)\phi(n)\).

Prove the \(AM-GM\) inequality for \(n=2\). Namely for two non-negative real numbers \(a\) and \(b\) we have \(2\sqrt{ab} \leq a+b\).

Consider an equilateral triangle \(ABC\). Parallel to each side, five equally spaced segments are drawn across the triangle so that \(ABC\) is subdivided into \(36\) smaller equilateral triangles. Vertices \(A,B\) and \(C\) are painted red, blue and green, respectively in counterclockwise order. Alice and Bob take turns painting each vertex of the smaller triangles either red, green, or blue with the following restrictions: the segment \(AB\) can only have red or green, the segment \(BC\) can only have green and blue, and the segment \(AC\) can only have blue and red. The interior vertices can be drawn freely. Once all vertices have been painted, Alice gets a point for every smaller triangle whose vertices have the three colors (red, green, and blue) appearing in the counterclockwise direction. Bob gets a point for every smaller triangle whose vertices have the three colors but in the clockwise direction. Who wins?

There are \(100\) people in a room, and each person has at least one friend in the room. Prove that amongst them there are two people with the same number of friends in the room (we don’t count being friends with oneself).

Can we obtain the polynomial \(h(x)=x\) by adding, subtracting, or multiplying the polynomials \(f(x)=x^2+x\) and \(g(x)=x^2+2\)?

The polynomial \(P(x)=x^3+3x^2-7x+1\) has three distinct roots: \(a,b,\) and \(c\). What is the value of \(a^2+b^2+c^2\)?

Find the remainder of dividing \(x^{100}-2x^{51}+1\) by \(x^2-1\). Try not to do a long calculation.