Problems

Katie and James take turns replacing the stars with any number of their choice in the following polynomial from left to right: \[x^4 +\star x^3+\star x^2+\star x+\star.\] Katie wins if once the game is over, the resulting polynomial has no integer roots (i.e: no roots which are whole numbers). Does James have a winning strategy?

Show that if a polynomial \(P(x)\) has an integer root (i.e: a root that is a whole number), then it can’t be that \(P(0)\) and \(P(1)\) are both odd.

Let \(x,x',y,y'\) be integers such that \(x+\sqrt{d}y=x'+\sqrt{d}y'\), where \(d\) is a number that is not a square. Show that \(x=x'\) and \(y=y'\).

Show that if \(u_1\) and \(u_2\) are solutions to Pell’s equation, then \(u_1u_2\) is also a solution to Pell’s equation. What can you conclude about the number of solutions, if there are any?

You have an \(8\times 8\) chessboard coloured in the usual way. You can pick any \(2\times 1\) or \(1\times 2\) piece and flip the white tiles to black tiles and vice-versa. Is it possible to finish with \(63\) white pieces and \(1\) black piece?

We start with the point \(S=(1,3)\) of the plane. We generate a sequence of points with coordinates \((x_n,y_n)\) with the following rule: \[x_0=1,y_0=3\qquad x_{n+1}=\frac{x_n+y_n}{2}\qquad y_{n+1}=\frac{2x_ny_n}{x_n+y_n}\] Is the point \((3,2)\) in the sequence?

Four black dots are drawn on a whiteboard. We write the numbers \(10,20,30,\) and \(40\) on top the dots and then play the following game: choose any of the four dots, subtract three from the number written on it, and then add one to the number written on top of each of the three other dots. After playing this game for some number of steps, can we make all four dots have the number \(25\) on top of them?

Jamie has a bag full of cards, where each card has a whole number written on it. How many cards must Jamie take from the bag to be certain that, among the cards chosen, there are at least two numbers whose average is also a whole number? Recall that to calculate the average of two numbers, we add them together and then divide by two.

The Pythagorean Theorem is one of the most important facts about geometry. It says that if we have a right-angled triangle (i.e: it has an angle of \(90^\circ\)), whose longest side measures \(C\), and its other two other sides measure \(A\) and \(B\):

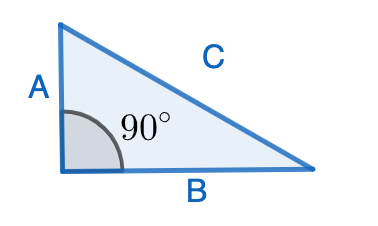
then \(A^2+B^2=C^2\). There are many proofs of this fact, and some involve dissections! Let’s have a look at the following two ways to dissect the same square:

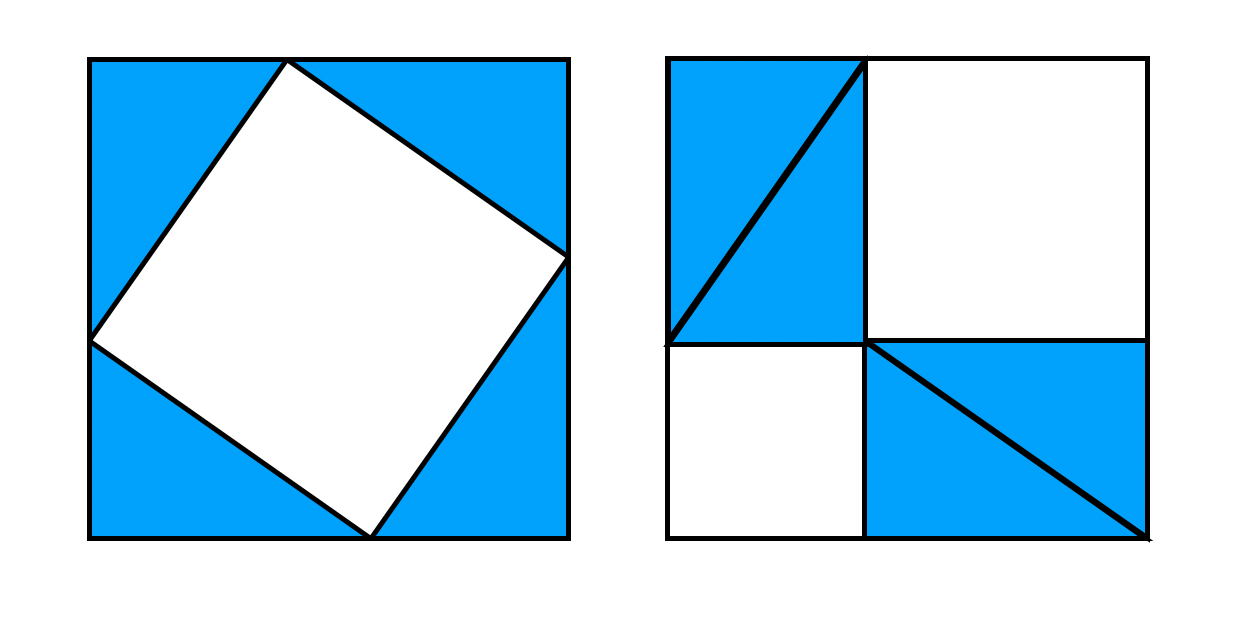
Can you explain how these dissections prove the Pythagorean Theorem?

A battle of the captains was held at a maths battle. The task was to write the smallest number that is divisible by \(60\) and it’s digits are only ’\(1\)’s or ’\(0\)’s. What is the answer?