Problems
Show that if \(a\) is a positive number, then \(a^3+2 \ge 2a \sqrt{a}\).
Is it possible to cover a \(6 \times 6\) board with the \(L\)-tetraminos without overlapping? The pieces can be flipped and turned.
Is it possible to cover a \(4n \times 4n\) board with the \(L\)-tetraminos without overlapping for any \(n\)? The pieces can be flipped and turned.
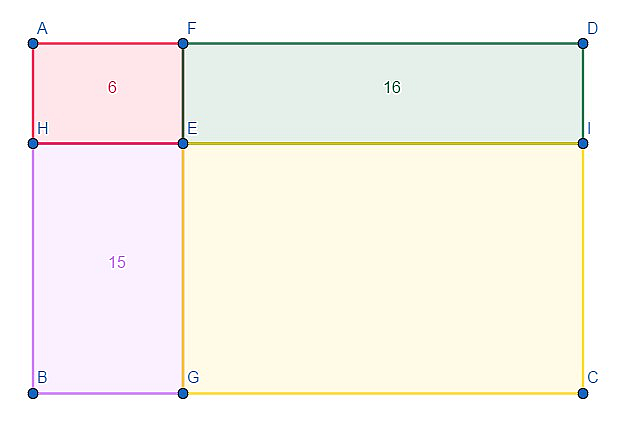
Each number denotes the area of a rectangle it is written into. What is the area of the last rectangle? (That is, the yellow one)
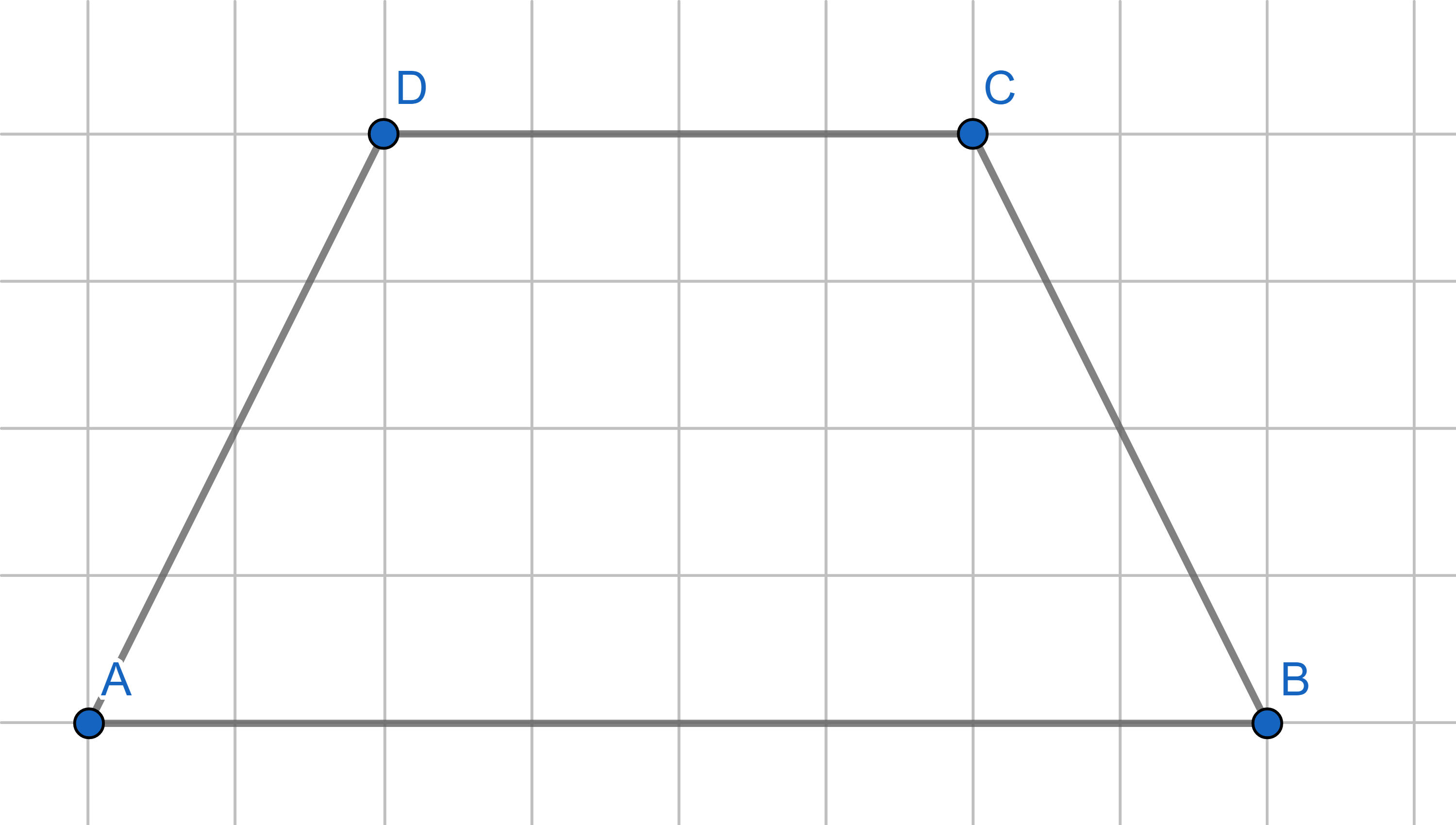
Divide the trapezium into two parts such that they can be reassembled to make a triangle.
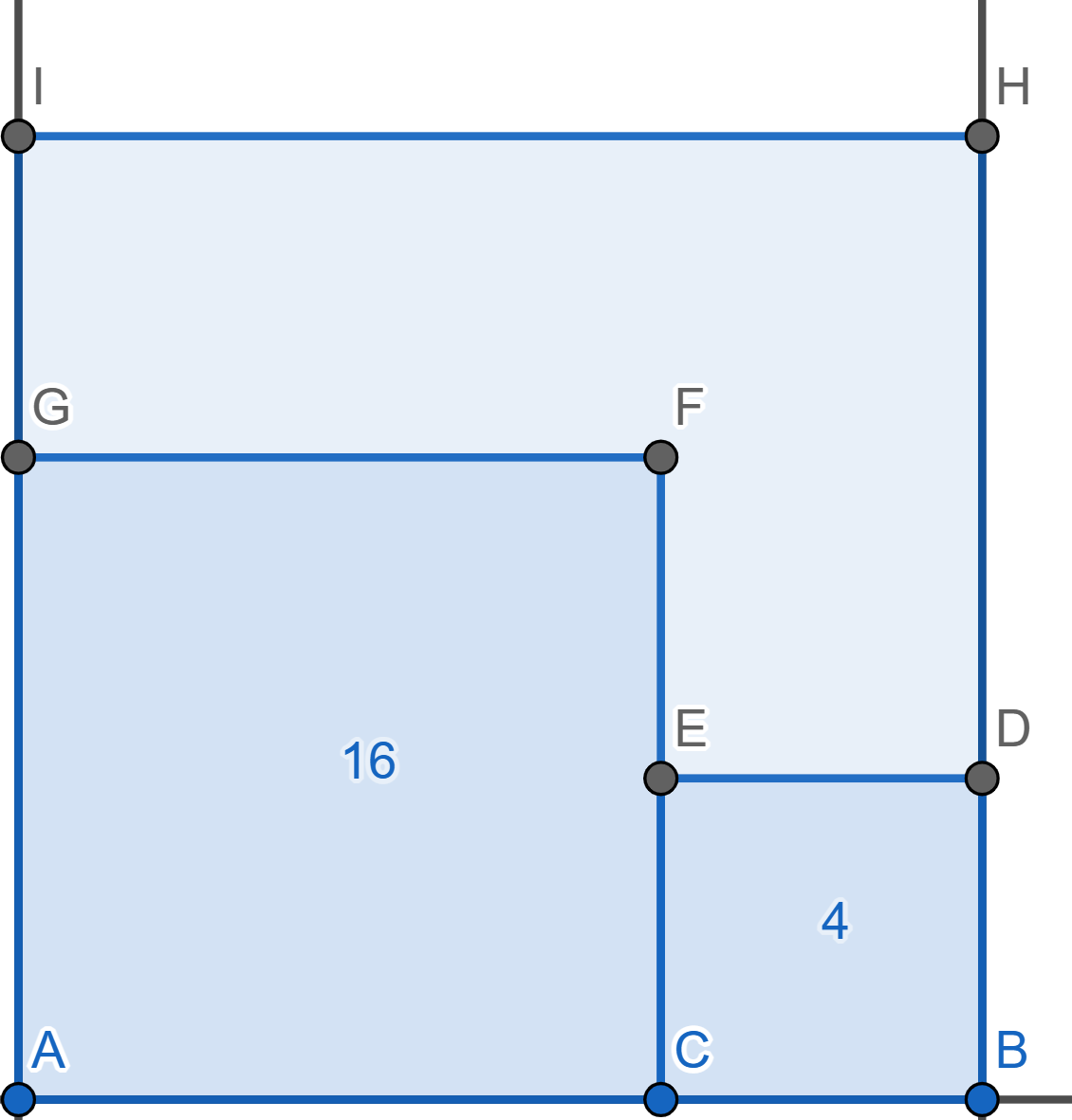
In a square \(ABHI\) two smaller squares are drawn: \(ACFG\) with area \(16\) and \(BCED\) with area \(4\). Find the area of hexagon \(DEFGIH\).
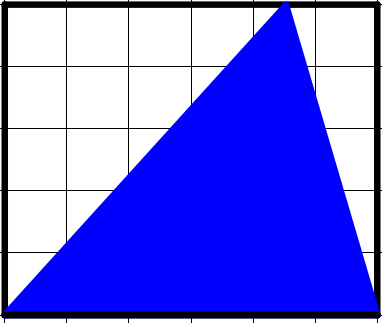
Each of the small squares has an area of \(1\). What is the area of the triangle?
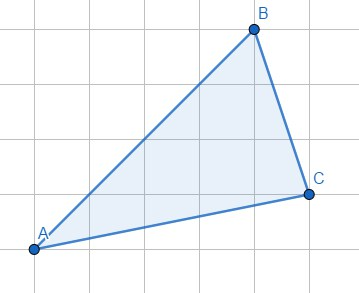
Divide the parallelogram into two parts such that they can be reassembled to make a triangle.
Charlie drew a triangle. Show a method of cutting this triangle into three parts which can then be reassembled into a rectangle - which works no matter what triangle he drew.