Problems

What is the ratio between the red and blue area? All shapes are semicircles and the red ones have equal radii.

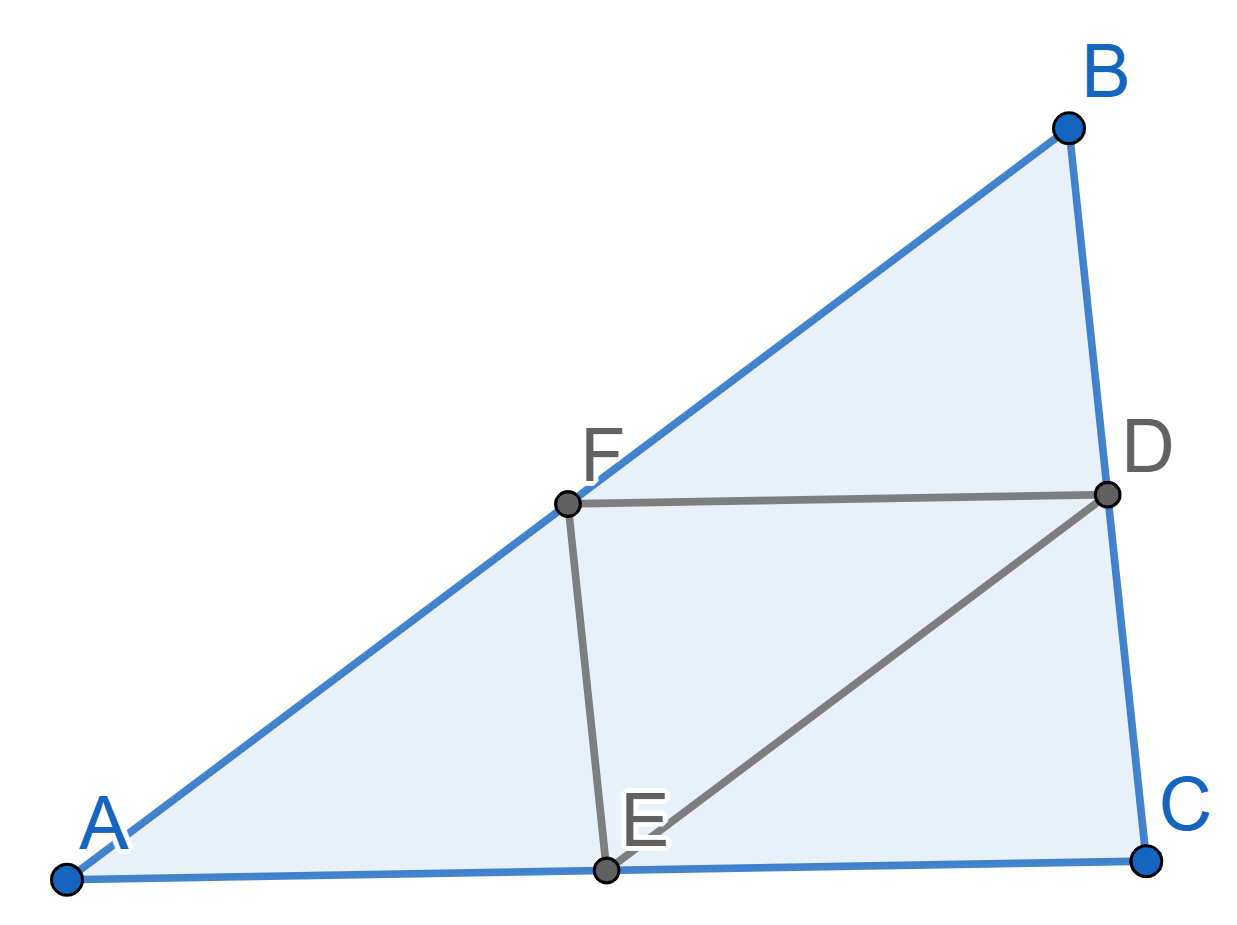
In a parallelogram \(ABCD\), point \(E\) belongs to the side \(CD\) and point \(F\) belongs to the side \(BC\). Show that the total red area is the same as the total blue area:

The figure below is a regular pentagram. What is larger, the black area or the blue area?

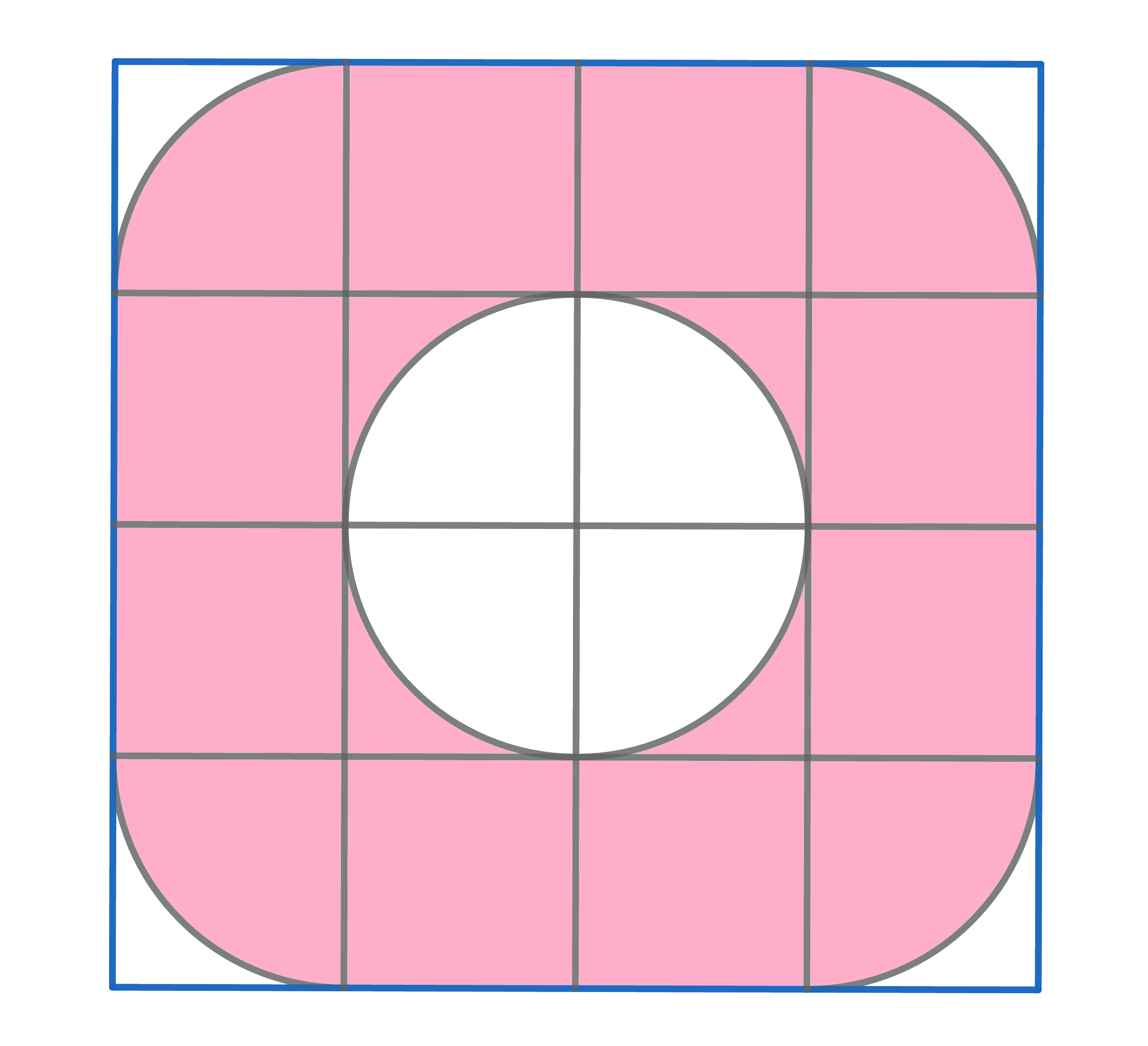
The area of the coloured figure equals \(48\)cm\(^2\). Find the length of the side of the smallest square.

The director of a bank has forgotten the combination to open the safe! He only remembers the first \(8\) out of \(10\) digits, and that the whole number was divisible by \(45\). Help him out and find all possible pairs of digits which could complete the combination. \[20242025**\]

There are two hourglasses, a small one and a large one. The sand in the small one takes \(7\) minutes to fall all the way through, and the sand in the large one takes \(11\) minutes. How can you measure \(15\) minutes using those?

The letters \(A\), \(R\), \(S\) and \(T\) represent different digits from \(1\) to \(9\). The same letters correspond to the same digits, while different letters correspond to different digits.
Find \(ART\), given that \(ARTS+STAR=10,T31\).

Let \(ABC\) be a triangle. Prove that the heights \(AD\), \(BE\), \(CF\) intersect in one point.

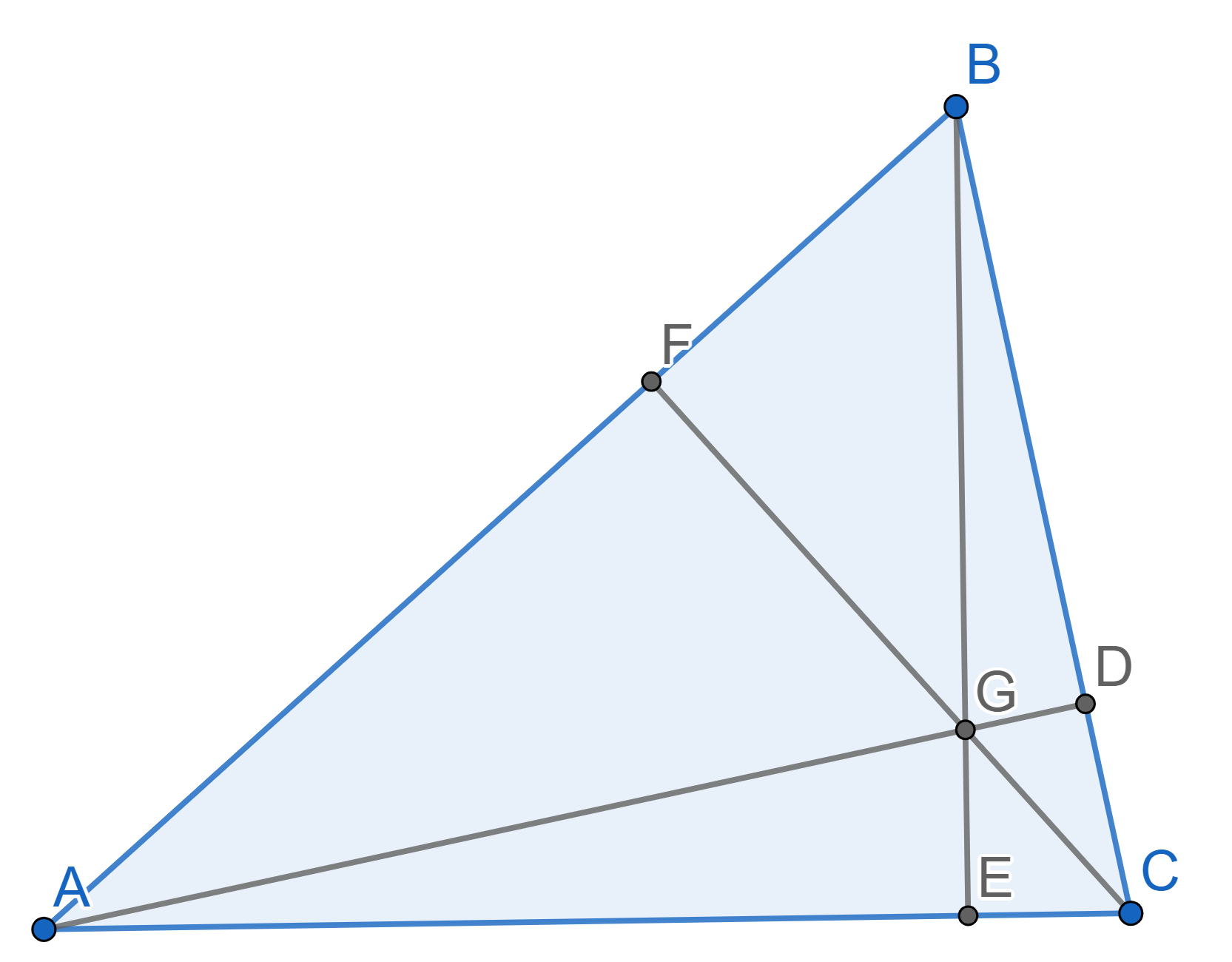
Let \(ABC\) be a triangle. Prove that the medians \(AD\), \(BE\), \(CF\) intersect in one point.

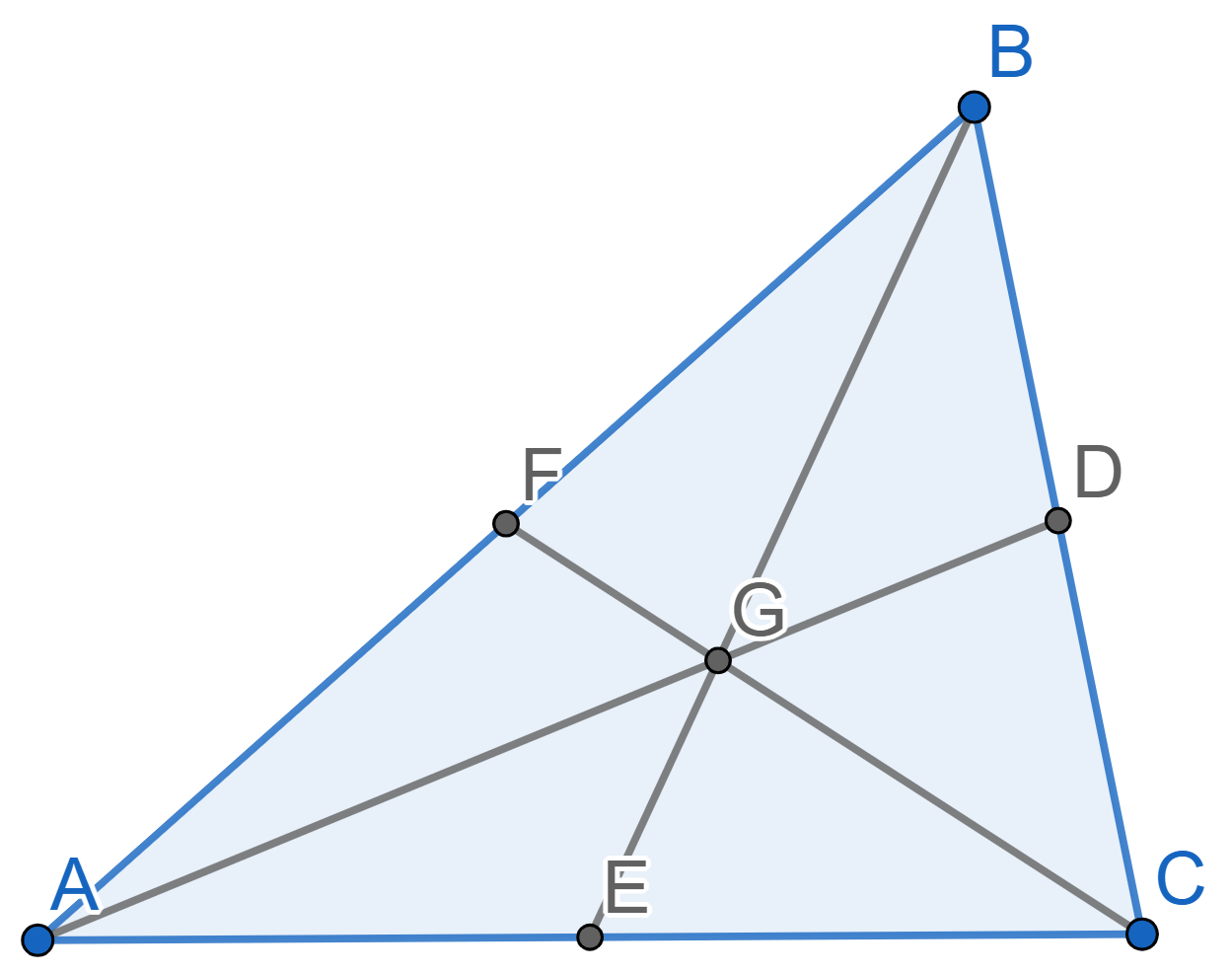
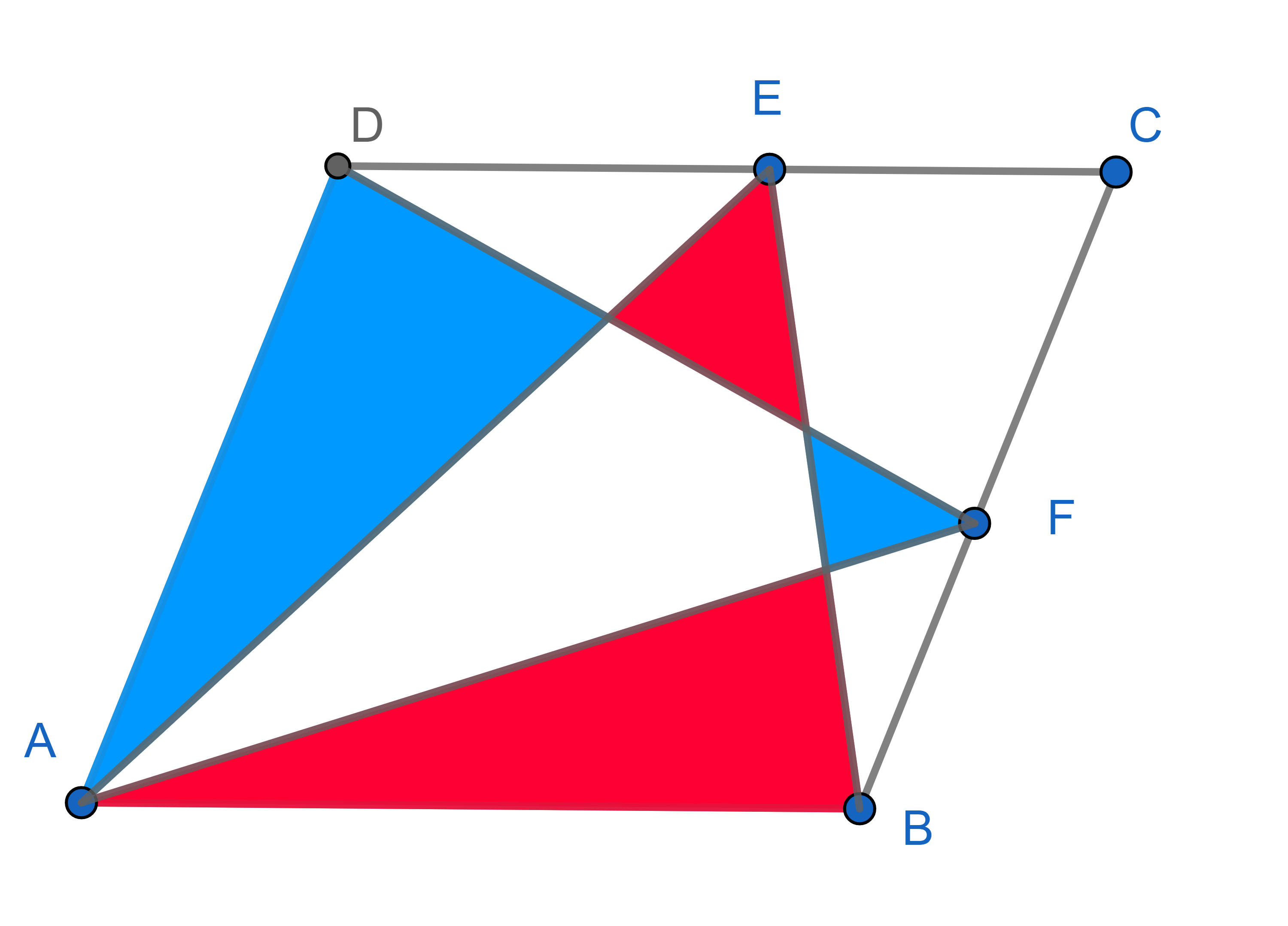
Let \(ABC\) be a triangle with medians \(AD\), \(BE\), \(CF\). Prove that the triangles \(ABC\) and \(DEF\) are similar. What is their similarity coefficient?