A \(1 \times 10\) strip is divided into unit squares. The numbers \(1, 2, \dots , 10\) are written into squares. First, the number 1 is written in one square, then the number 2 is written into one of the neighboring squares, then the number 3 is written into one of the neighboring squares of those already occupied, and so on (the choice of the first square is made arbitrarily and the choice of the neighbor at each step). In how many ways can this be done?
On a plane there is a square, and invisible ink is dotted at a point \(P\). A person with special glasses can see the spot. If we draw a straight line, then the person will answer the question of on which side of the line does \(P\) lie (if \(P\) lies on the line, then he says that \(P\) lies on the line).
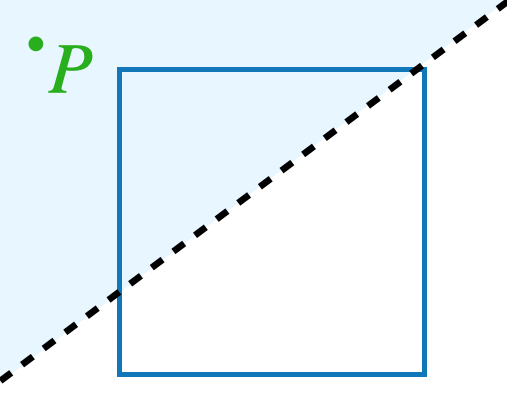
What is the smallest number of such questions you need to ask to find out if the point \(P\) is inside the square?
A cube with side length of 20 is divided into 8000 unit cubes, and on each cube a number is written. It is known that in each column of 20 cubes parallel to the edge of the cube, the sum of the numbers is equal to 1 (the columns in all three directions are considered). On some cubes a number 10 is written. Through this cube there are three layers of \(1 \times 20 \times 20\) cubes, parallel to the faces of the cube. Find the sum of all the numbers outside of these layers.
Two people are playing. The first player writes out numbers from left to right, randomly alternating between 0 and 1, until there are 2021 numbers in total. Each time after the first one writes out the next digit, the second switches two numbers from the already written row (when only one digit is written, the second misses its move). Is the second player always able to ensure that, after his last move, the arrangement of the numbers is symmetrical relative to the middle number?
In Conrad’s collection there are four royal gold five-pound coins. Conrad was told that some two of them were fake. Conrad wants to check (prove or disprove) that among the coins there are exactly two fake ones. Will he be able to do this with the help of two weighings on weighing scales without weights? (Counterfeit coins are the same in weight, real ones are also the same in weight, but false ones are lighter than real ones.)
Janine and Zahara each thought of a natural number and said them to Alex. Alex wrote the sum of the thought of numbers onto one sheet of paper, and on the other – their product, after which one of the sheets was hidden, and the other (on it was written the number of 2002) was shown to Janine and Zahara. Seeing this number, Janine said that she did not know what number Zahara had thought of. Hearing this, Zahara said that she did not know what number Janine had thought of. What was the number which Zahara had thought of?
On a table there are 2022 cards with the numbers 1, 2, 3, ..., 2022. Two players take one card in turn. After all the cards are taken, the winner is the one who has a greater last digit of the sum of the numbers on the cards taken. Find out which of the players can always win regardless of the opponent’s strategy, and also explain how he should go about playing.
The case of Brown, Jones and Smith is being considered. One of them committed a crime. During the investigation, each of them made two statements. Brown: “I did not do it. Jones did not do it. " Smith: “I did not do it. Brown did it. “Jones:" Brown did not do it. This was done by Smith. “Then it turned out that one of them had told the truth in both statements, another had lied both times, and the third had told the truth once, and he had lied once. Who committed the crime?
Replace the letters with digits in a way that makes the following sum as big as possible: \[SEND +MORE +MONEY.\]
Jane wrote another number on the board. This time it was a two-digit number and again it did not include digit 5. Jane then decided to include it, but the number was written too close to the edge, so she decided to t the 5 in between the two digits. She noticed that the resulting number is 11 times larger than the original. What is the sum of digits of the new number?