We solve problems

Problems Algebra and arithmetic Number theory. Divisibility

Prove that \(n^2 + 1\) is not divisible by \(3\) for any natural \(n\).

Problems Set theory and logic Mathematical logic Mathematical logic (other)

Two weighings. There are 7 coins which are identical on the surface, including 5 real ones (all of the same weight) and 2 counterfeit coins (both of the same weight, but lighter than the real ones). How can you find the 3 real coins with the help of two weighings on scales without weights?

Problem #PRU-102862

Problems Set theory and logic Theory of algotithms Theory of algorithms (other)

10–12 2.0

Multiplication of numbers. Restore the following example of the multiplication of natural numbers if it is known that the sum of the digits of both factors is the same.

Problem #PRU-102863

Problems Set theory and logic Theory of algotithms Theory of algorithms (other)

10–12 2.0

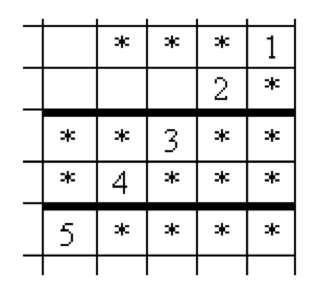
Restore the example of the multiplication.

Problem #PRU-102883

Problems Algebra and arithmetic Combinatorics

12–14 2.0

Prove that the number of all arrangements of the largest possible amount of peaceful bishops (figures that move on diagonals and don’t threaten each other) on the \(8\times 8\) chessboard is an exact square.

Problem #PRU-103009

Problems Set theory and logic Theory of algotithms Theory of algorithms (other)

10–12 2.0

There are 6 locked suitcases and 6 keys to them. At the same time, it is not known to which suitcase each key fits. What is the smallest number of attempts you need to make in order to open all the suitcases for sure? And how many attempts will it take there are not 6 but 10 keys and suitcases?

Problem #PRU-103027

Problems Set theory and logic Theory of algotithms Theory of algorithms (other)

10–12 2.0

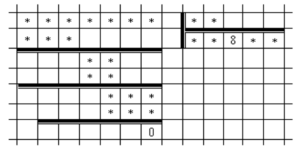
Decipher the following rebus (see the figure). Despite the fact that only two figures are known here, and all others are replaced by asterisks, the example can be restored.

Problem #PRU-103729

Problems Algebra and arithmetic Number theory. Divisibility Odd and even numbers

10–12 2.0

The parliament of a certain country has two houses with an equal number of members. In order to make a decision on an important issue all the members voted and there were no abstentions. When the chairman announced that the decision had been taken with a 23-vote advantage, the opposition leader declared that the results had been rigged. How did he know it?

Problem #PRU-103757

Problems Algebra and arithmetic Algebraic equations and systems of equations Higher order equations. Palindromic polynomial equations Equations of higher order (other) Calculus Real numbers Integer and fractional parts. Archimedean property

12–14 2.0

A resident of one foreign intelligence agency informed the centre about the forthcoming signing of a number of bilateral agreements between the fifteen former republics of the USSR. According to his report, each of them will conclude an agreement exactly with three others. Should this resident be trusted?

Problem #PRU-103803

Problems Set theory and logic Theory of algotithms Theory of algorithms (other)

10–12 2.0

Three people A, B, C counted a bunch of balls of four colors (see table).

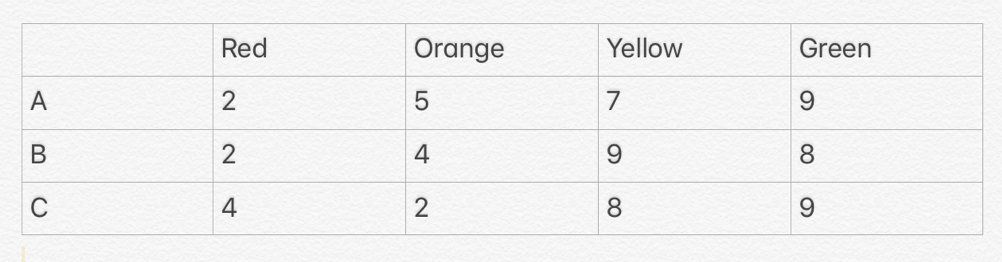
Each of them correctly distinguished some two colors, and confused the numbers of the other two colours: one mixed up the red and orange, another – orange and yellow, and the third – yellow and green. The results of their calculations are given in the table.

How many balls of each colour actually were there?