Problems

The bank of the Nile was approached by a group of six people: three Bedouins, each with his wife. At the shore is a boat with oars, which can withstand only two people at a time. A Bedouin can not allow his wife to be without him whilst in the company of another man. Can the whole group cross to the other side?

Solve problem number 108736 for the inscription \(A\), \(BC\), \(DEF\), \(CGH\), \(CBE\), \(EKG\).

Replace \(a, b\) and \(c\) with integers not equal to \(1\) in the equality \((ay^b)^c = - 64y^6\), so it would become an identity.

Prove that for all \(x \in (0;\pi /2)\) for \(n > m\), where \(n, m\) are natural, we have the inequality \(2 | \sin^n x-\cos^n x | \leq 3 | \sin^m x-\cos^m x |\);

Members of the State parliament formed factions in such a way that for any two factions \(A\) and \(B\) (not necessarily different)

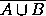
– also a faction (through

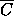
the set of all parliament members not included in \(C\) is denoted). Prove that for any two factions \(A\) and \(B\), \(A \cup % \includegraphics{https://problems-static.s3.eu-west-2.amazonaws.com/static/test/task_images/82/109909-3.png} B\) is also a faction.

A New Year’s garland, hanging along the school corridor, consists of red and blue light bulbs. Next to each red light bulb there must necessarily be a blue one. What is the largest number of red light bulbs in this garland, if it consists of only 50 light bulbs?

A magician with a blindfold gives a spectator five cards with the numbers from 1 to 5 written on them. The spectator hides two cards, and gives the other three to the assistant magician. The assistant indicates to the spectator two of them, and the spectator then calls out the numbers of these cards to the magician (in the order in which he wants). After that, the magician guesses the numbers of the cards hidden by the spectator. How can the magician and the assistant make sure that the trick always works?

In 10 boxes there are pencils (there are no empty boxes). It is known that in different boxes there is a different number of pencils, and in each box, all pencils are of different colors. Prove that from each box you can choose a pencil so that they will all be of different colors.

Which numbers can stand in place of the letters in the equality \(AB \times C = DE\), if different letters denote different numbers and from left to right the numbers are written in ascending order?

There are 40 weights of weights of 1 g, 2 g, ..., 40 grams. Of these, 10 weights of even weight were chosen and placed on the left hand side of the scales. Then we selected 10 weights of odd weight and put it on the right hand side of the scales. The scales were balanced. Prove that on one of the bowls of the scales there are two weights with a mass difference of 20 g.