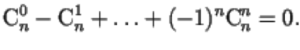Problems
Prove that a graph with \(n\) vertices, the degree of each of which is at least \(\frac{n-1}{2}\), is connected.
In the Far East, the only type of transport is a carpet-plane. From the capital there are 21 carpet-planes, from the city of Dalny there is one carpet-plane, and from all of the other cities there are 20. Prove that you can fly from the capital to Dalny (possibly with interchanges).
In a country coming out of each city there are 100 roads and from each city it is possible to reach any other. One road was closed for repairs. Prove that even now you can get from every city to any other.
a) Two in turn put bishops in the cells of a chessboard. The next move must beat at least one empty cell. The bishop also beats the cell in which it is located. The player who loses is the one who cannot make a move.
b) Repeat the same, but with rooks.
There are two piles of sweets: one with 20 sweets and the other with 21 sweets. In one go, one of the piles needs to be eaten, and the second pile is divided into two not necessarily equal piles. The player that cannot make a move loses. Which player wins and which one loses?
The game begins with the number 0. In one go, it is allowed to add to the actual number any natural number from 1 to 9. The winner is the one who gets the number 100.
Solve the equation with integers \(x^2 + y^2 = 4z - 1\).
Prove that out of \(n\) objects an even number of objects can be chosen in \(2^{n-1}\) ways.
Prove that every number \(a\) in Pascal’s triangle is equal to
a) the sum of the numbers of the previous right diagonal, starting from the leftmost number up until the one to the right above the number \(a\).
b) the sum of the numbers of the previous left diagonal, starting from the leftmost number to the one to left of the number which is above \(a\).