Problems

Let \(n\ge3\) be a positive integer. A regular \(n\)-gon is a polygon with \(n\) sides where every side has the same length, and every angle is the same. For example, a regular \(3\)-gon is an equilateral triangle, and a regular \(4\)-gon is a square.

What symmetries does a regular \(n\)-gon have, and how many?

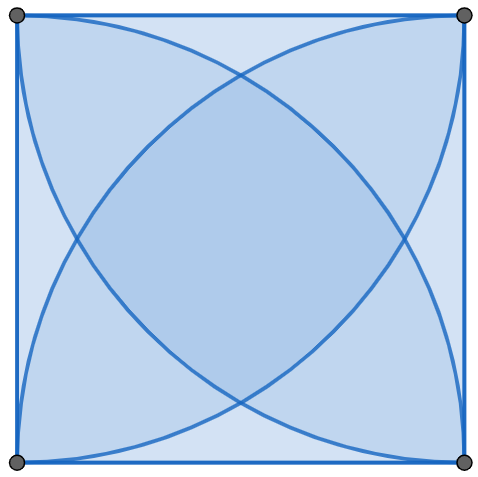
We have a square of side length 1. At each vertex of the square, we draw a circle of radius 1. What is the area bounded by all four circles?

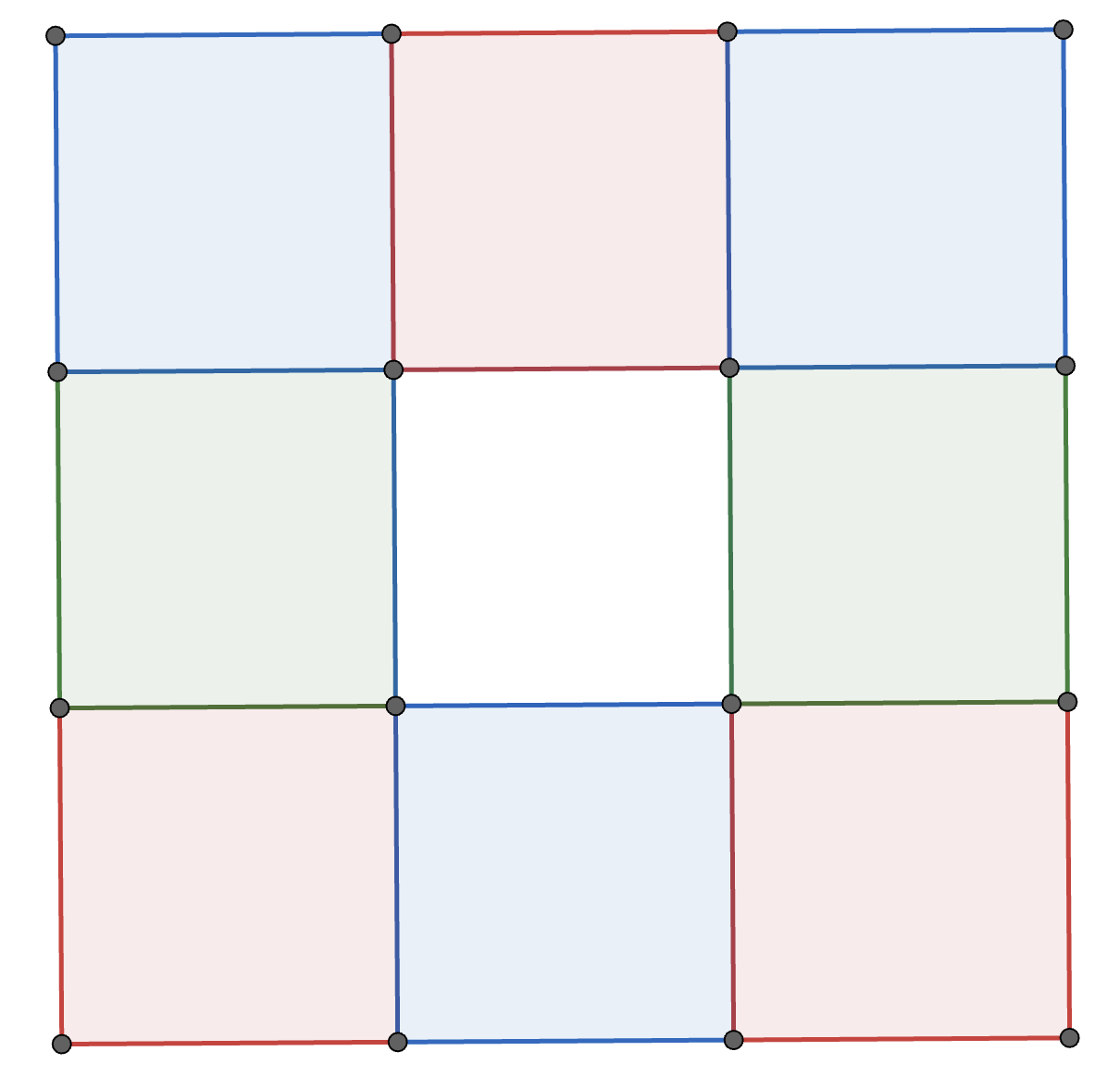
Each square in a \(3\times3\) grid of squares is coloured red, white, blue, or green so that every \(2\times2\) square contains one square of each color. One such colouring is shown below. How many different colourings are possible?

For any positive integer \(k\), the factorial \(k!\) is defined as a product of all integers between 1 and \(k\) inclusive: \(k! = k \times (k-1) \times ... \times 1\). What’s the remainder when \(2025!+2024!+2023!+...+3!+2!+1!\) is divided by \(8\)?

Show that a rotation about an axis on a sphere followed by a rotation about a different axis is again a rotation about some axis.

Let \(u\) and \(v\) be two positive integers, with \(u>v\). Prove that a triangle with side lengths \(u^2-v^2\), \(2uv\) and \(u^2+v^2\) is right-angled.

We call a triple of natural numbers (also known as positive integers) \((a,b,c)\) satisfying \(a^2+b^2=c^2\) a Pythagorean triple. If, further, \(a\), \(b\) and \(c\) are relatively prime, then we say that \((a,b,c)\) is a primitive Pythagorean triple.

Show that every primitive Pythagorean triple can be written in the form \((u^2-v^2,2uv,u^2+v^2)\) for some coprime positive integers \(u>v\).

The lengths of three sides of a right-angled triangle are all integers.

Show that one of them is divisible by \(5\).

There are two imposters and seven crewmates on the rocket ‘Plus’. How many ways are there for the nine people to split into three groups of three, such that each group has at least two crewmates? The two imposters and seven crewmates are all distinguishable from each other, but we’re not concerned with the order of the three groups.

For example: \(\{I_1,C_1,C_2\}\), \(\{I_2,C_3,C_4\}\) and \(\{C_5,C_6,C_7\}\) is the same as \(\{C_3,C_4,I_2\}\), \(\{C_5,C_6,C_7\}\) and \(\{I_1,C_2,C_1\}\) but different from \(\{I_2,C_1,C_2\}\), \(\{I_1,C_3,C_4\}\) and \(\{C_5,C_6,C_7\}\).

King Hattius has three prisoners and gives them the following puzzle. He will put a randomly coloured hat on each of their heads: red, blue or green. He’ll then give them \(10\) seconds for them to each guess their own hat’s colour at the same time.

However! Each prisoner can only see the other two prisoners’ hats, not their own. There are no mirrors in the prison, and they are not allowed to take off their hat, nor talk, mouth, use sign-language, or otherwise communicate with the other two prisoners during those ten seconds.

Hattius tells them that he’ll release them all if at least one correctly guesses their hat’s colour. He gives them an hour to come up with a strategy - what should their strategy be?