We solve problems

Problems Geometry Plane geometry Area Triangle area

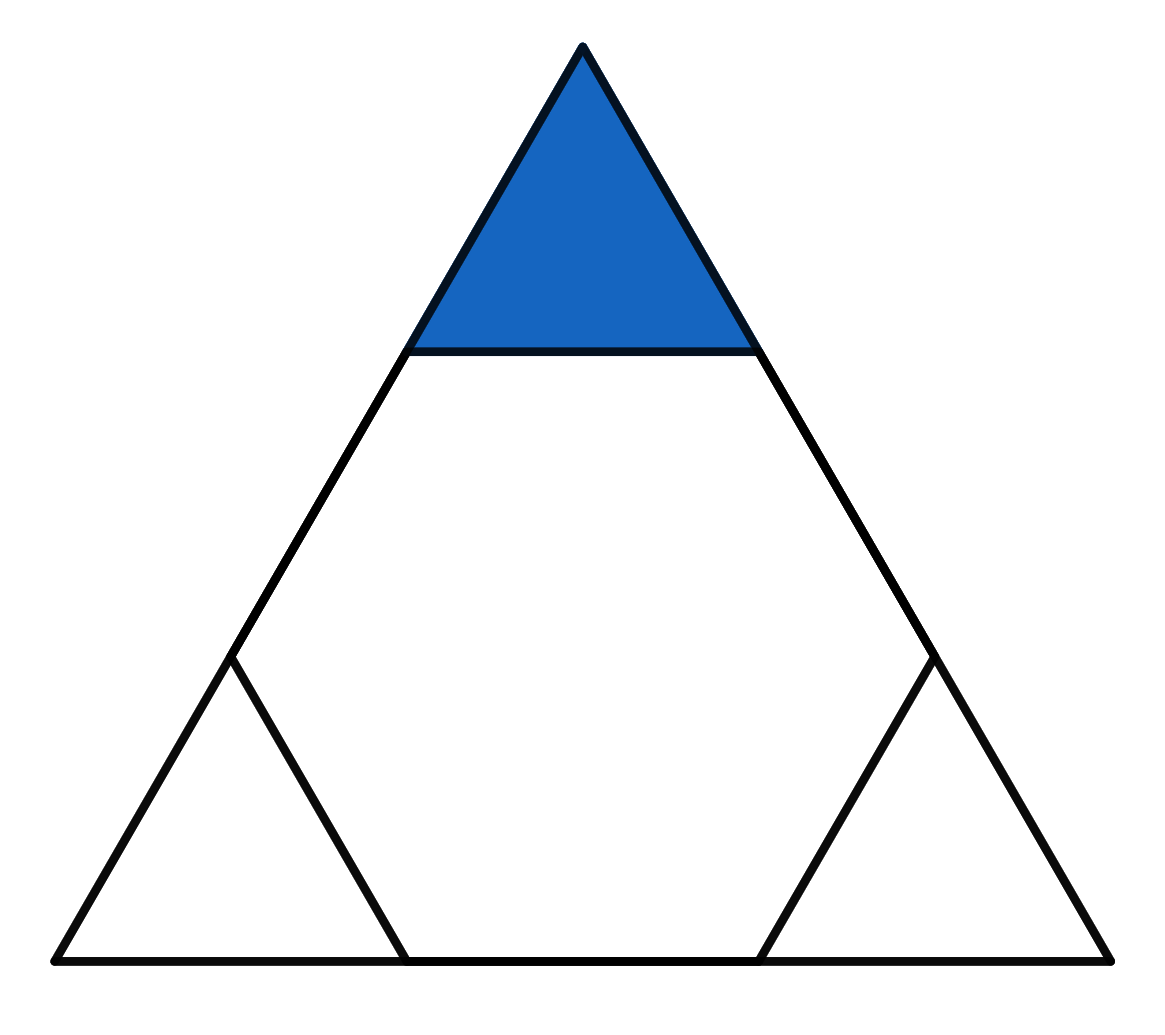
The triangle visible in the picture is equilateral. The hexagon inside is a regular hexagon. If the area of the whole big triangle is \(18\), find the area of the small blue triangle.

Problem #PRU-7650

Problems Geometry Plane geometry Area Area of a circle, sector, segment

11–13 3.0

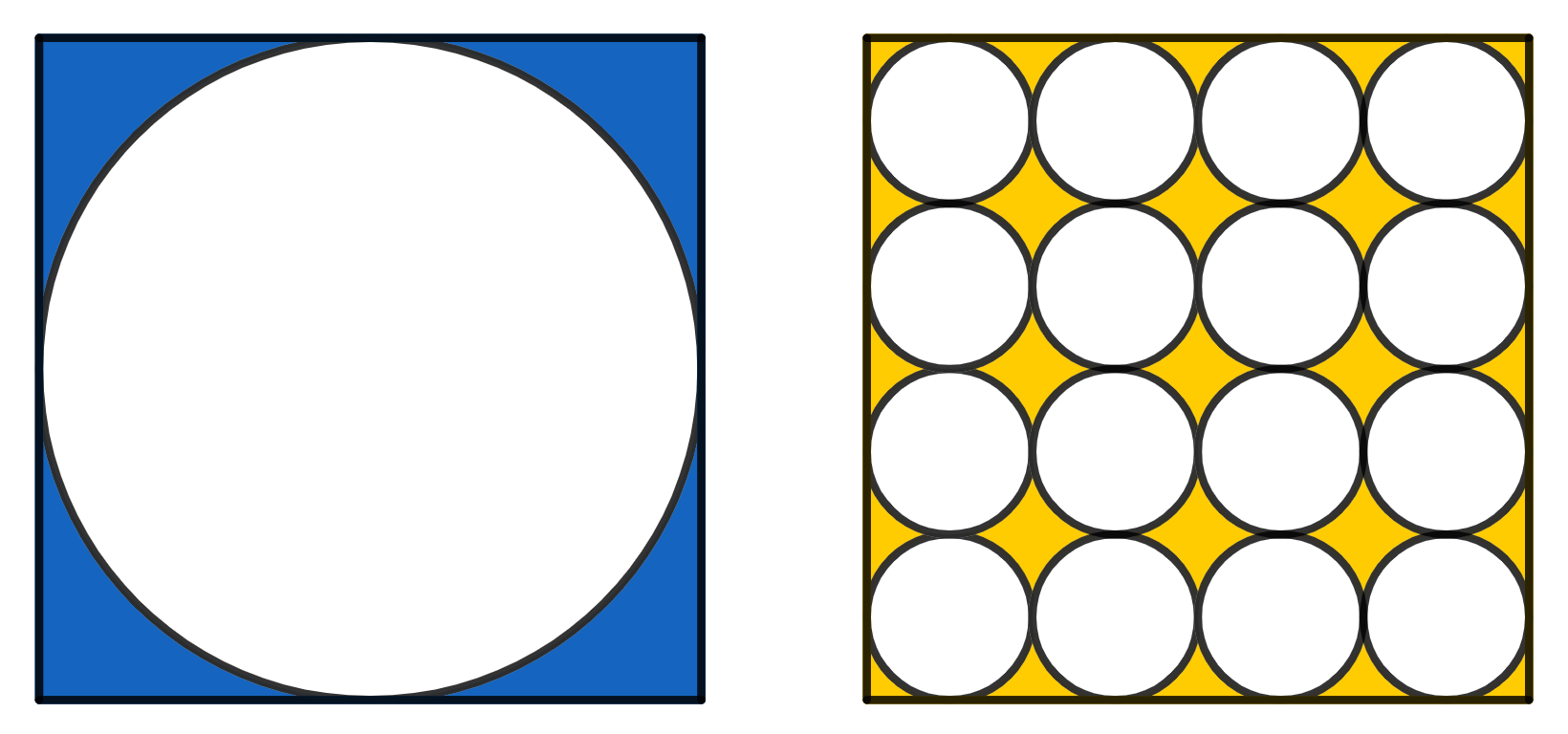
On the left there is a circle inscribed in a square of side 1. On the right there are 16 smaller, identical circles, which all together fit inside a square of side 1. Which area is greater, the yellow or the blue one?

Problem #PRU-76543

Problems Number Theory Divisibility Division with remainders. Arithmetic of remainders Division with remainder Methods Pigeonhole principle Pigeonhole principle (other)

12–15 3.0

Prove that, for any integer \(n\), among the numbers \(n, n + 1, n + 2, \dots , n + 9\) there is at least one number that is mutually prime with the other nine numbers.

Problem #PRU-78206

Problems Methods Algebraic methods Counting in two ways Pigeonhole principle Pigeonhole principle (other)

13–14 3.0

30 pupils in years 7 to 11 each created at least one maths problem, making 40 maths problems altogether. Every possible pair of pupils in the same year created the same number of problems. Every possible pair of pupils in different years created a different number of problems. How many pupils created exactly one problem?

Problem #PRU-78475

Problems Geometry Plane geometry Lines, segments, rays, and angles

13–14 3.0

You are given \(7\) straight lines on a plane, no two of which are parallel. Prove that there will be two lines such that the angle between them is less than \(26^{\circ}\).

Problem #PRU-78494

Problems Number Theory Divisibility Division with remainders. Arithmetic of remainders Division with remainder Methods Pigeonhole principle Pigeonhole principle (other)

12–15 3.0

Every integer from 1 to 64 is written in an \(8 \times 8\) table. Prove that no matter the order these numbers are written, there are two adjacent numbers which are at least \(5\) apart. (Numbers in cells which share a side are called adjacent).

Problem #PRU-78501

Problems Methods Pigeonhole principle Pigeonhole principle (other)

14–15 3.0

All of the integers from 1 to 81 are written in a \(9 \times 9\) table. Prove that in this case there are two adjacent numbers, the difference between which is not less than 6. (Numbers that are in cells which share a common side are called adjacent.)

Problem #PRU-78508

Problems Number Theory Numeral systems Decimal number system Methods Pigeonhole principle Pigeonhole principle (other)

14–16 3.0

Prove that in a group of 11 arbitrary infinitely long decimal numbers, it is possible to choose two whose difference contains either, in decimal form, an infinite number of zeroes or an infinite number of nines.

Problem #PRU-78529

Graph theory Problems Methods Pigeonhole principle Pigeonhole principle (other)

12–14 3.0

A group of \(2n\) people were gathered together. Each person knew at least \(n\) of the other people present. Prove that it is possible to select 4 people and seat them around a table so that each person sits next to people they know. (\(n \geq 2\))

Problem #PRU-78552

Problems Methods Pigeonhole principle Pigeonhole principle (other) Fun Problems Word Problems Tables and tournaments Tournament tables

12–14 3.0

30 teams are taking part in a football championship. Prove that at any moment in the contest there will be two teams who have played the same number of matches up to that moment, assuming every team plays every other team exactly once by the end of the tournament.