Problems

Three segments whose lengths are equal to \(a, b\) and \(c\) are given. Using only straightedge and compass construct a segment of length: a) \(ab/c\); b) \(\sqrt {ab}\).

Solve the equations in integers:

a) \(3x^2 + 5y^2 = 345\);

b) \(1 + x + x^2 + x^3 = 2^y\).

In honor of the March 8 holiday, a competition of performances was organized. Two performances reached the final. \(N\) students of the 5th grade played in the first one and \(n\) students of the 4th grade played in the second one. The performance was attended by \(2n\) mothers of all \(2n\) students. The best performance is chosen by a vote of the mothers. It is known that half of the mothers vote honestly, i.e. for the performance that was truly better and the mothers of the other half in any case vote for the performance in which their child participates.

a) Find the probability of the best performance winning by a majority of votes.

b) The same question but this time more than two performances made it to the final.

A square \(4 \times 4\) is called magic if all the numbers from 1 to 16 can be written into its cells in such a way that the sums of numbers in columns, rows and two diagonals are equal to each other. Sixth-grader Edwin began to make a magic square and written the number 1 in certain cell. His younger brother Theo decided to help him and put the numbers \(2\) and \(3\) in the cells adjacent to the number \(1\). Is it possible for Edwin to finish the magic square after such help?

Is it possible to cut such a hole in \(10\times 10 \,\,cm^2\) piece of paper, though which you can step?

The meeting of the secret agents took place in the green house.

Considering the numbers in the windows of the green house, what should be drawn in the empty frame?

Pinoccio keeps his Golden Key in the safe that is locked with a numerical password. For secure storage of the Key he replaced some digits in the password by letters (in such a way that different letters substitute different digits). After replacement Pinoccio got the password \(QUANTISED17\). Honest John found out that:
• the number \(QUANTISED\) is divisible by all integers less than 17, and
• the difference \(QUA-NTI\) is divisible by \(7\).
Could he find the password?

Decipher the quote from Philip Pullmans "His Dark Materials":
Erh csy wlepp orsa xli xvyxl, erh xli xvyxl wlepp qeoi csy jvii.
The same letters correspond to the same in the phrase, different letters correspond to different. We know that no original letters stayed in place, meaning that in places of e,r,h there was surely something else.

Cut the "biscuit" into 16 congruent pieces. The sections are not necessarily rectilinear.

In the middle of an empty pool there is a square platform of \(50 \times 50\) cm, split into cells of \(10\times 10\) cm. Sunny builds towers of \(10\times 10\times 10\)cm cubes on the platform cells. After that his friend Margo turns on the water and counts how many towers are still above the water level. They call each visible tower an island.

For example, let’s consider the case when the heights of the towers are as given in the table on the right. Then at the water level of \(5\) cm there is \(1\) island, at the water level of \(15\) cm there are two islands (if the islands have a common corner or don’t intersect at all, they are considered separate islands), and at the water level of \(25\) cm, all the towers are covered with water and there are \(0\) islands.

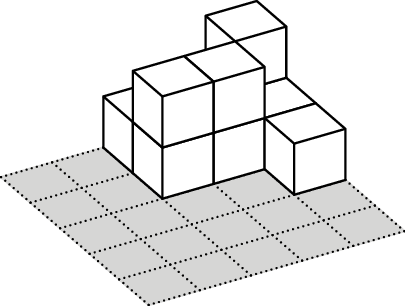
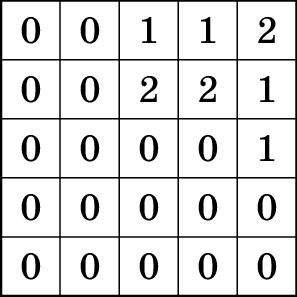
Find out how Sunny should build his towers to get the following numbers of islands corresponding to the level of water in the pool: \[\begin{array}{@{}*{26}{c}@{}} \textit{Water level (cm)}& 5& 15& 25& 35& 45\\ \textit{Number of islands}& 2& 5& 2& 5& 0 \end{array}\]

In the solution, write down how many cubes are there composing a tower in each cell as it is done in the example.