Problems
Using \(R(s,t)\le R(s-1,t)+R(s,t-1)\), prove that \(R(k,k)\le 4^k\).
Two players are playing a game. The first player is thinking of a finite sequence of positive integers \(a_1\), \(a_2\), ..., \(a_n\). The second player can try to find the first player’s sequence by naming their own sequence \(b_1\), \(b_2\), ..., \(b_n\). After this, the first player will give the result \(a_1b_1 + a_2b_2 + ...+a_nb_n\). Then the second player can say another sequence \(c_1\), \(c_2\), ..., \(c_n\) to get another answer \(a_1c_1+ a_2c_2 + ... +a_nc_n\) from the first player. Find the smallest number of sequences the second player has to name to find out the sequence \(a_1\), \(a_2\), ..., \(a_n\).
Let \(ABC\) be a non-isosceles
triangle. The point \(G\) is the point
of intersection of the medians \(AE\),
\(BF\), \(CD\). The point \(H\) is the point of intersection of all
heights. The point \(I\) is the center
of the circumscribed circle of \(ABC\),
or the point of intersection of all perpendicular bisectors to the
segments \(AB\), \(BC\), \(AC\).
Prove that points \(I,G,H\) lie on one
line and that the ratio \(IG:GH =
1:2\). The line that all of \(I\), \(G\)
and \(H\) lie on is called the
Euler line of triangle \(ABC\).
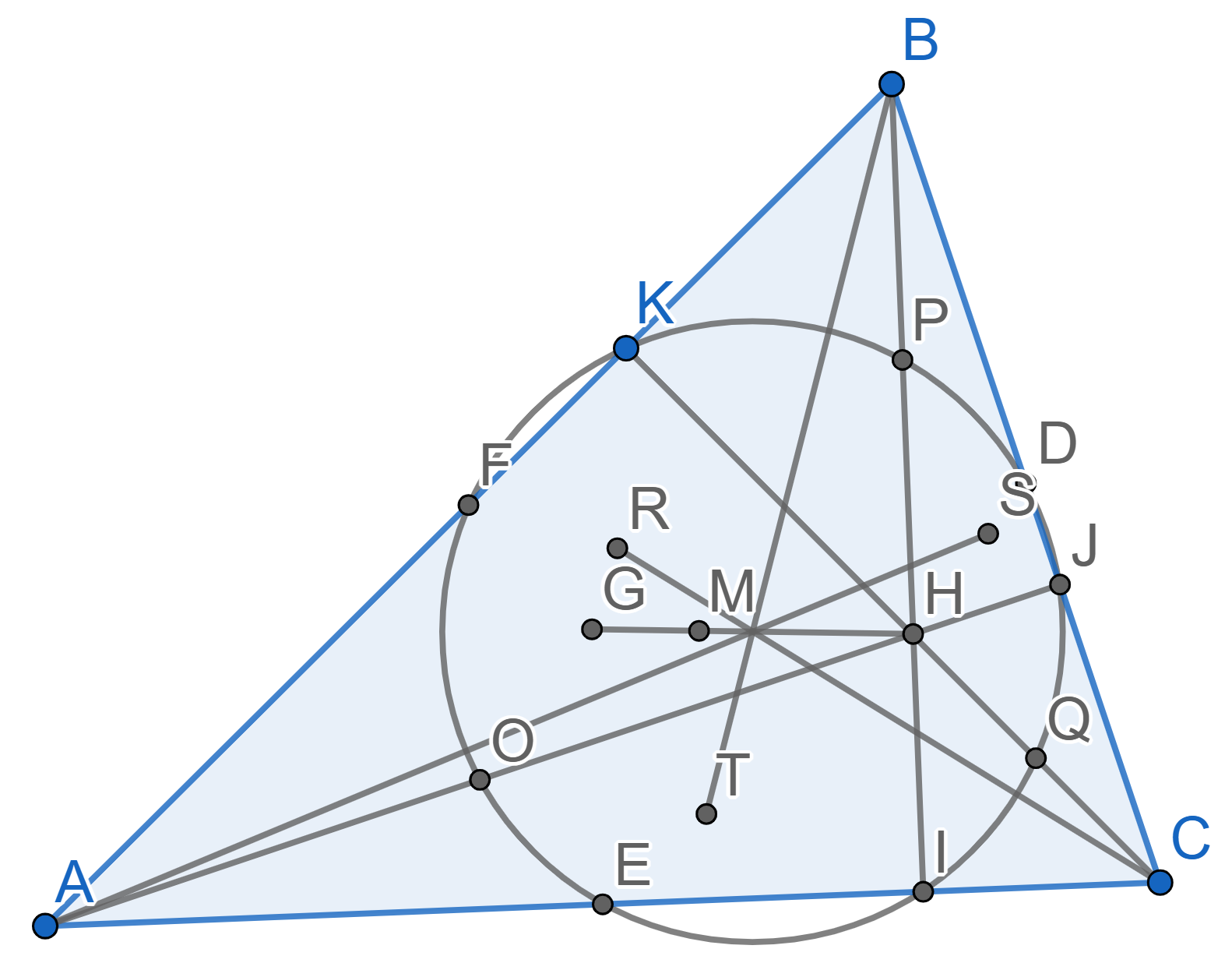
Let \(ABC\) be a triangle with midpoints \(D\) on the side \(BC\), \(E\) on the side \(AC\) and \(F\) on the side \(AB\). Let \(M\) be the point of intersection of all medians of the triangle \(ABC\) and let \(H\) be the point of intersection of the heights \(AJ\), \(BI\) and \(CK\). Consider the Euler circle of the triangle \(ABC\), which is the one that contains the points \(D,J,I,E,F,K\). This circle intersects the segments \(AH\), \(BH\) and \(CH\) at the points \(O\), \(P\) and \(Q\) respectively. Prove that \(O\), \(P\) and \(Q\) are the midpoints of the segments \(AH\), \(BH\) and \(CH\).
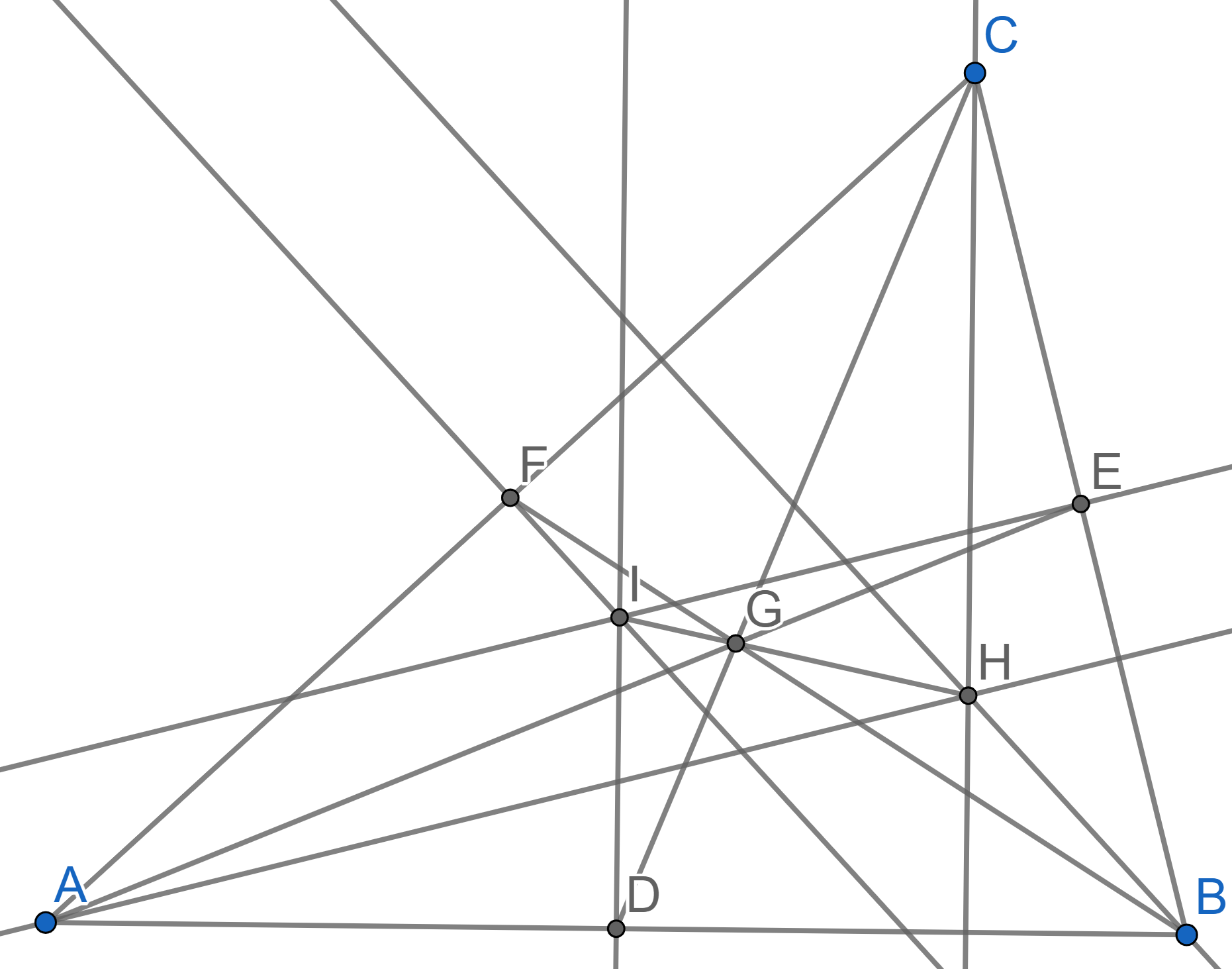
Consider the point \(H\) of intersection of the heights of the triangle \(ABC\). Prove that Euler lines of the triangles \(ABC\), \(ABH\), \(BCH\) and \(ACH\) intersect at one point. On the diagram below the points \(R,S,T\) are the points of intersection of medians in triangles \(ABH\), \(BCH\), and \(ACH\) respectively.
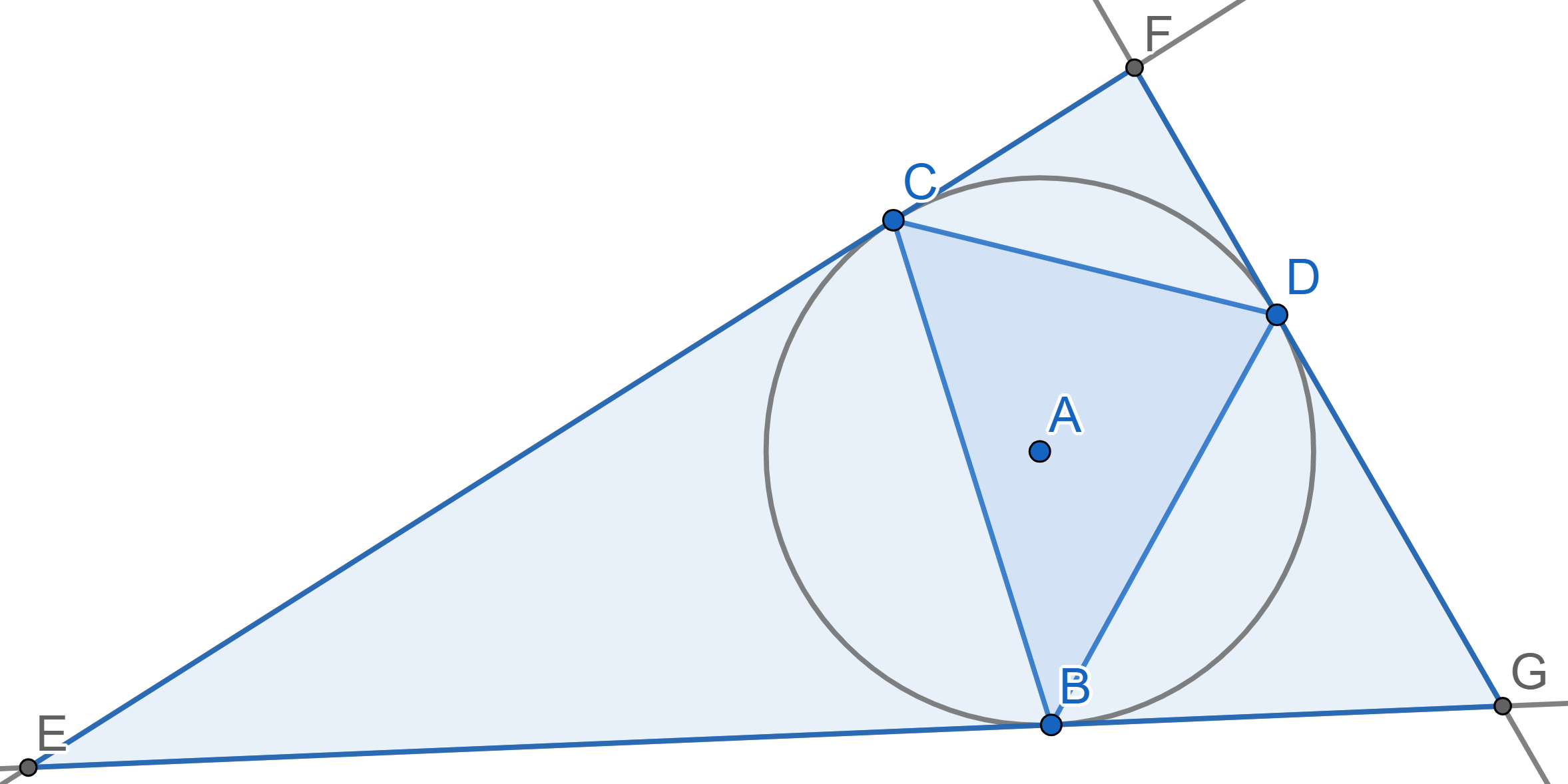
Consider the triangle \(BCD\), inscribed in a circle with center \(A\). The segments \(EF\), \(FG\) and \(EG\) are tangent to the circle at the points \(C\), \(D\) and \(B\) respectively. Prove that the Euler line of the triangle \(BCD\) passes through the center of the circle circumscribed around the triangle \(EFG\).
Find all pairs \((x,n)\) of positive integers such that \(x^n + 2^n + 1\) is a divisor of \(x^{n+1} + 2^{n+1} + 1\).
Let \(\phi(n)\) be Euler’s function. Namely \(\phi(n)\) counts how many integers from \(1\) to \(n\) inclusive are coprime with \(n\). For two natural numbers \(m\), \(n\) such that \(\gcd(m,n)=1\), prove that \(\phi(mn) = \phi(m)\phi(n)\).
Let \(a,b,c >0\) be positive real numbers with \(abc \leq 1\). Prove that \[\frac{a}{c} + \frac{b}{a} + \frac{c}{b} \geq a+b+c.\]