Problems

From IMO 1999. Let \(n\geq 2\) be an integer. Determine the least possible constant \(C\) such that the inequality \[\sum_{1\leq i<j\leq n} x_ix_j(x_i^2 + x_j^2) \leq C(\sum_{1\leq i\leq n}x_i)^4\] holds for all non-negative real numbers \(x_i\). For this constant \(C\) find out when the equality holds.

Proposed by USA for IMO 1993. For positive real numbers \(a,b,c,d\) prove that \[\frac{a}{b+2c+3d} + \frac{b}{c+2d+3a} + \frac{c}{d+2a+3b} + \frac{d}{a+2b+3c} \geq \frac{2}{3}.\]

Prove the \(AM-GM\) inequality for positive real numbers \(a_1\), \(a_2\), ..., \(a_n\): \[\frac{a_1+a_2+...+a_n}{n}\geq \sqrt[n]{a_1a_2...a_n}.\]

Due to Paul Erdős. Each of the positive integers \(a_1\), \(a_2\), ..., \(a_n\) is less than \(1951\). The least common multiple of any two of these integers is greater than \(1951\). Prove that \[\frac{1}{a_1} + ... + \frac{1}{a_n} < 1+ \frac{n}{1951}.\]

Sperner’s lemma in dimension \(2\).
Subdivide a triangle \(ABC\) arbitrarily into a triangulation consisting of smaller triangles meeting edge to edge. Define Sperner coloring of the triangulation as an assignment of three colors to the vertices of the triangulation such that:

• Each of the three vertices \(A, B,\) and \(C\) of the initial triangle has a distinct color

• The vertices that lie along any edge of triangle \(ABC\) have only two colors, the two colors at the endpoints of the edge. For example, each vertex on \(AC\) must have the same color as \(A\) or \(C.\)

Here is an example of Sperner’s triangulation

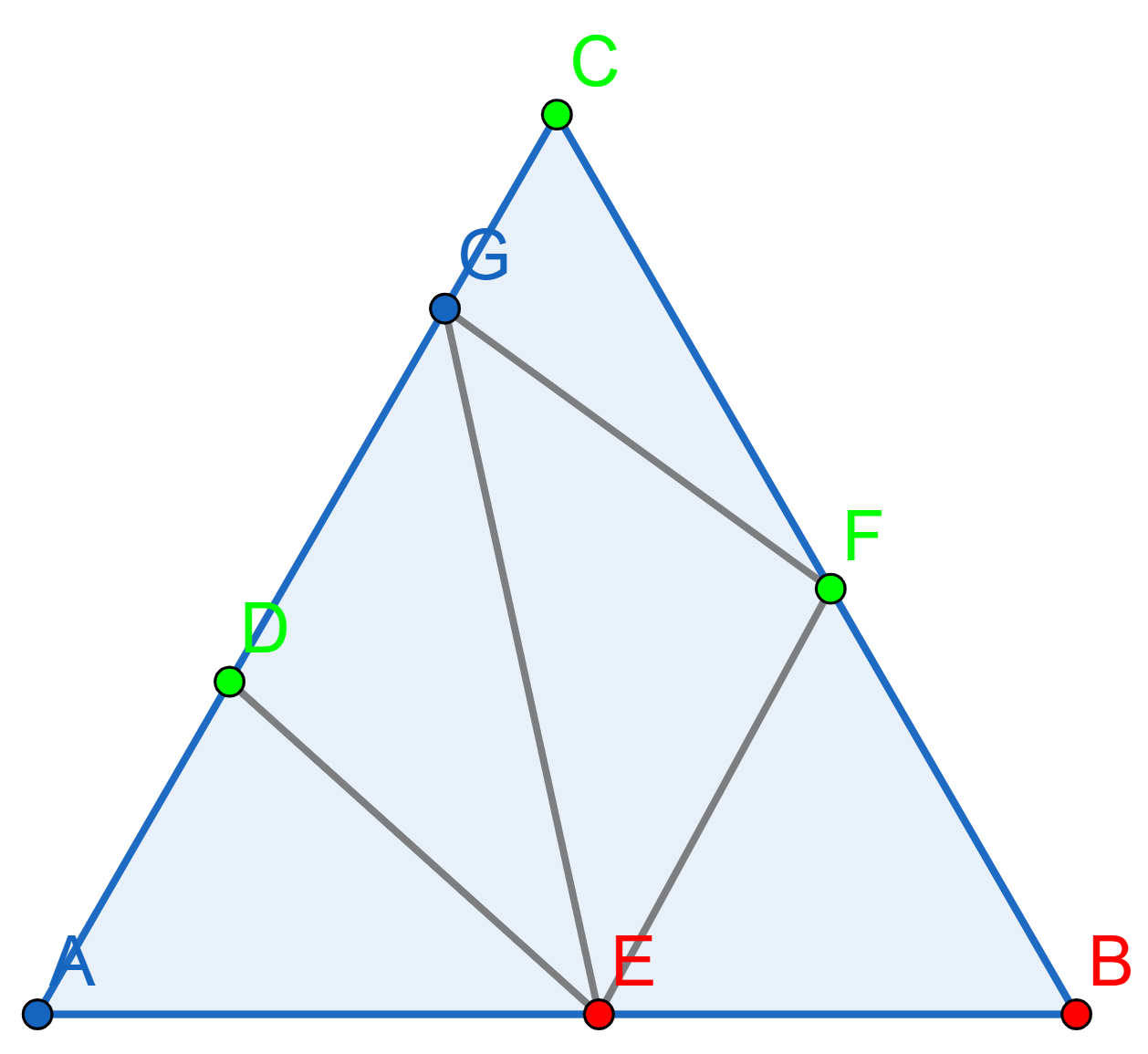
Prove that every Sperner coloring of every triangulation has at least one "rainbow triangle", a smaller triangle in the triangulation that has its vertices colored with all three different colors. More precisely, there must be an odd number of rainbow triangles.

Prove the general version of Sperner’s lemma: Consider an \(n\)-dimensional simplex \(\mathcal{A} = A_1A_2...A_{n+1}\). Strictly speaking a simplex is a convex linear combination of \(n+1\) points in general position (when \(k\) points are never in one subspace of dimension \(k-1\)). One can view it as an \(n\)-dimensional tetrahedron or a body spanned over vertices \((0,0,...,0), (1,0,0,...,0), (0,1,0,0...,0), ... (0,0,...0,1)\). \[\mathcal{A} = \{\sum_{i=1}^{n+1}a_i(0,0,...,1,...,0), \,\,\, a_i \geq 0, \,\,\,\, \sum_{i=1}^{n+1}a_i = 1\}.\]

A simplicial subdivision of an \(n\)-dimensional simplex \(\mathcal{A}\) is a partition of \(\mathcal{A}\) into small simplices (cells) of the same dimension, such that any two cells are either disjoint, or they share a full face of a certain dimension.
Define a Sperner’s coloring of a simplicial subdivision as an assignment of \(n+1\) colors to the vertices of the subdivision, so that the vertices of \(\mathcal{A}\) receive all different colors, and points on each face of \(\mathcal{A}\) use only the colors of the vertices defining the respective face of \(\mathcal{A}\).
Prove that every Sperner’s coloring of any subdivision of an \(n\)-dimensional simplex contains an odd number of rainbow simplexes, namely whose vertices are colored using all \(n+1\) colors.

Prove that the only solution to \(5^a-3^b=2\) with \(a,b\) being positive integers is \(a=b=1\).

Show that Pell’s equation \(x^2-dy^2=1\) has a nontrivial solution.

Without using any wolves, show that Robinson’s goat can only graze shapes that are convex (that means, whenever you pick two points inside the shape, the whole line between them also lies inside). But if Robinson is allowed to use as many wolves as he likes, this restriction disappears. Show that in this case, he can make the goat graze in the shape of any polygon at all.

In a field, there are two pegs, \(A\) and \(B\), placed \(15\) metres apart. Each peg has a small ring on top, and a rope can slide freely through these rings. You have one rope and two goats that want to graze the grass, but they will fight each other if they can both reach the same spot.

The rope may be arranged in any way you choose: it could pass through both rings, only one, or neither, depending on your setup. For what lengths of rope can you arrange things so that the goats cannot fight each other?