Problems
Find all the functions \(f\colon \mathbb {R} \rightarrow \mathbb {R}\) which satisfy the inequality \(f (x + y) + f (y + z) + f (z + x) \geq 3f (x + 2y + 3z)\) for all \(x, y, z\).
Find the sum \(1/3 + 2/3 + 2^2/3 + 2^3/3 + \dots + 2^{1000}/3\).
A number set \(M\) contains \(2003\) distinct positive numbers, such that for any three distinct elements \(a, b, c\) in \(M\), the number \(a^2 + bc\) is rational. Prove that we can choose a natural number \(n\) such that for any \(a\) in \(M\) the number \(a\sqrt{n}\) is rational.
A numeric set \(M\) containing 2003 distinct numbers is such that for every two distinct elements \(a, b\) in \(M\), the number \(a^2+ b\sqrt 2\) is rational. Prove that for any \(a\) in \(M\) the number \(q\sqrt 2\) is rational.
Is there a bounded function \(f\colon \mathbb{R} \rightarrow \mathbb{R}\) such that \(f (1)> 0\) and \(f (x)\) satisfies the inequality \(f^2 (x + y) \geq f^2 (x) + 2f (xy) + f^2 (y)\) for all \(x, y \in \mathbb{R}\)?
For which \(\alpha\) does there exist a function \(f\colon \mathbb{R} \rightarrow \mathbb{R}\) that is not a constant, such that \(f (\alpha (x + y)) = f (x) + f (y)\)?
On a function \(f (x)\) defined on the whole line of real numbers, it is known that for any \(a > 1\) the function \(f (x)\) + \(f (ax)\) is continuous on the whole line. Prove that \(f (x)\) is also continuous on the whole line.
Does there exist a function \(f (x)\) defined for all \(x \in \mathbb{R}\) and for all \(x, y \in \mathbb{R}\) satisfying the inequality \(| f (x + y) + \sin x + \sin y | < 2\)?
The real numbers \(x\) and \(y\) are such that for any distinct prime odd \(p\) and \(q\) the number \(x^p + y^q\) is rational. Prove that \(x\) and \(y\) are rational numbers.
The functions \(f (x) - x\) and \(f (x^2) - x^6\) are defined for all positive \(x\) and increase. Prove that the function
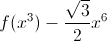
also increases for all positive \(x\).