We solve problems

Problems Geometry Plane geometry Area Area ratio Finding the area by rearrangment

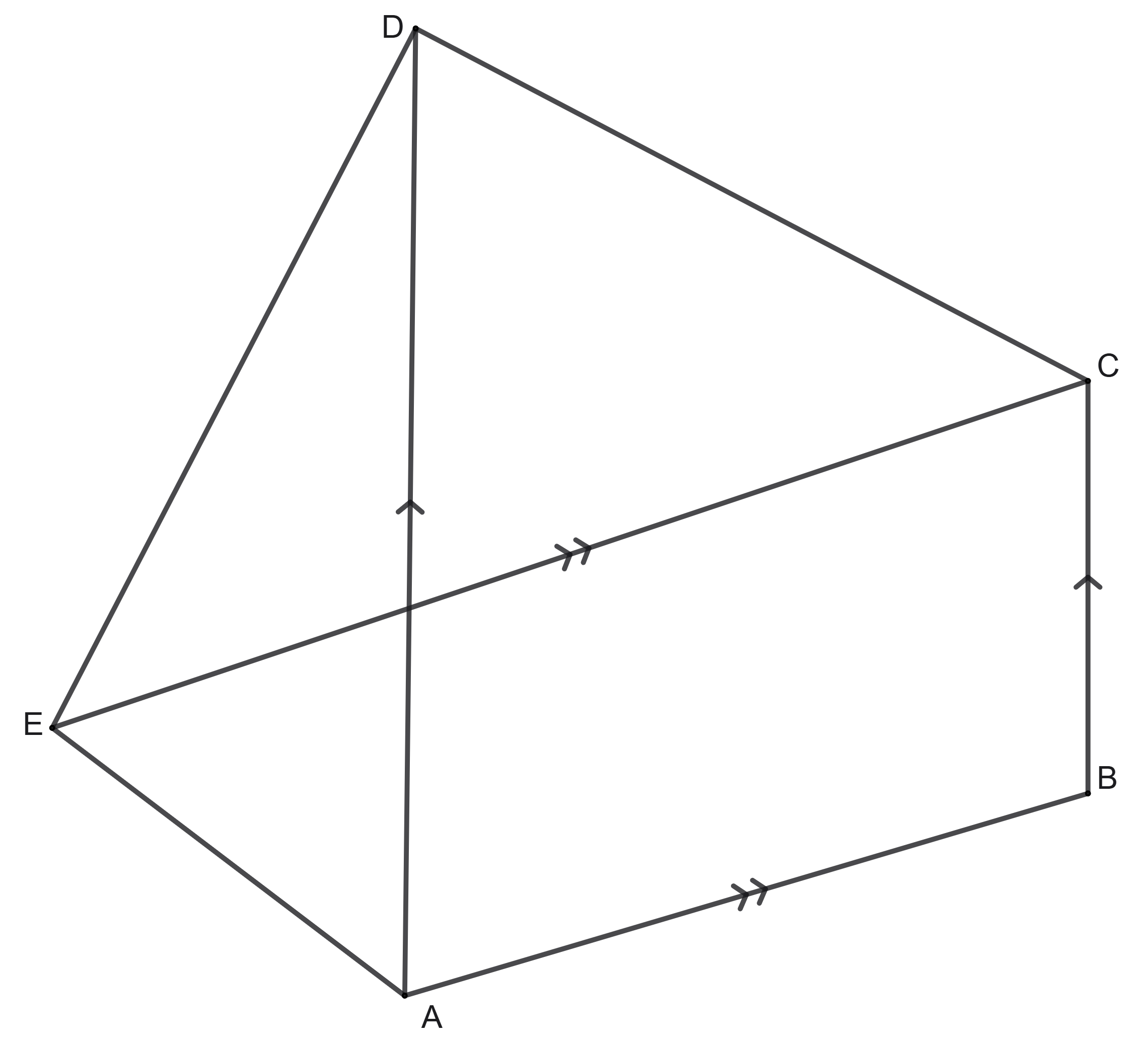
In a pentagon \(ABCDE\), diagonal \(AD\) is parallel to the side \(BC\) and the diagonal \(CE\) is parallel to the side \(AB\). Show that the areas of the triangles \(\triangle ABE\) and \(\triangle BCD\) are the same.

Problem #PRU-77894

Problems Number Theory Divisibility Division with remainders. Arithmetic of remainders Arithmetic of remainders Methods Pigeonhole principle Pigeonhole principle (other)

13–14 4.0

If we are given any 100 whole numbers then amongst them it is always possible to choose one, or several of them, so that their sum gives a number divisible by 100. Prove that this is the case.

Problem #PRU-78043

Problemas Métodos Métodos de cálculo Monotonía y acotación Principio del casillero Principio del casillero (otros) Álgebra Polinomios Polinomios cuadráticos

13–15 4.0

The expression \(ax^2+bx+c\) is an exact fourth power for all integers \(x\). Prove that \(a=b=0\).

Problem #PRU-78051

Problemas Cálculo Números reales Partes enteras y fraccionarias. Propiedad arquimediana Métodos Principio del casillero Principio del casillero (otros)

13–15 4.0

The numbers \(\lfloor a\rfloor, \lfloor 2a\rfloor, \dots , \lfloor Na\rfloor\) are all different, and the numbers \(\lfloor 1/a\rfloor, \lfloor 2/a\rfloor,\dots , \lfloor M/a\rfloor\) are also all different. Find all such \(a\).

Problem #PRU-78086

Problemas Métodos Principio del casillero Principio del casillero (número finito de puntos, líneas, etc.)

13–15 4.0

2022 points are selected from a cube, whose edge is equal to 13 units. Is it possible to place a cube with edge of 1 unit in this cube so that there is not one selected point inside it?

Problem #PRU-78234

Problemas Métodos Principio del palomar Métodos algebraicos Procesos y operaciones

13–15 4.0

The number \(A\) is divisible by \(1, 2, 3, \dots , 9\). Prove that if \(2A\) is presented in the form of a sum of some natural numbers smaller than 10, \(2A= a_1 +a_2 +\dots +a_k\), then we can always choose some of the numbers \(a_1, a_2, \dots , a_k\) so that the sum of the chosen numbers is equal to \(A\).

Problem #PRU-78259

Problemas Métodos Ejemplos y contraejemplos. Pruebas constructivas Principio de casillas Principio de casillas (otro)

14–16 4.0

A table of \(4\times4\) cells is given, in some cells of which a star is placed. Show that you can arrange seven stars so that when you remove any two rows and any two columns of this table, there will always be at least one star in the remaining cells. Prove that if there are fewer than seven stars, you can always remove two rows and two columns so that all the remaining cells are empty.

Problem #PRU-78270

Problemas Geometría Geometría plana Área Área de formas curvilíneas Métodos Principio del casillero Principio del casillero (área y volumen)

13–15 4.0

120 unit squares are placed inside a \(20 \times 25\) rectangle. Prove that it will always be possible to place a circle with diameter 1 inside the rectangle, without it overlapping with any of the unit squares.

Problem #PRU-78496

Problemas Métodos Ejemplos y contraejemplos. Pruebas constructivas Principio del casillero Principio del casillero (otros)

13–14 4.0

What is the largest amount of numbers that can be selected from the set 1, 2, ..., 1963 so that the sum of any two numbers is not divisible by their difference?

Problem #PRU-78557

Problems Discrete Mathematics Combinatorics Dissections, partitions, covers and tilings Covers Methods Extremal principle Extremal principle (other) Pigeonhole principle Pigeonhole principle (other)

13–15 4.0

Several pieces of carpet are laid along a corridor. Pieces cover the entire corridor from end to end without omissions and even overlap one another, so that over some parts of the floor lie several layers of carpet. Prove that you can remove a few pieces, perhaps by taking them out from under others and leaving the rest exactly in the same places they used to be, so that the corridor will still be completely covered and the total length of the pieces left will be less than twice the length corridor.