Problems

Jess and Tess are playing a game colouring points on a blank plane. Jess is moving first, she picks a non-colored point on a plane and colours it red. Then Tess makes a move, she picks \(2022\) colourless points on the plane and colours them all green. Jess then moves again, and they take turns. Jess wins if she manages to create a red equilateral triangle on the plane, Tess is trying to prevent that from happening. Will Jess always eventually win?

Can you cover a \(13 \times 13\) square using \(2 \times 2\) and \(3 \times 3\) squares?

A \((2n - 1) \times (2n - 1)\) board is tiled with pieces of the following possible types:

Prove that at least \(4n-1\) of the first type have been used.

Two circles with centres \(A\) and \(C\) are tangent to each other at the point \(B\). Both circles are tangent to the sides of an angle with vertex \(D\). It is known that the angle \(\angle EDF = 60^{\circ}\) and the radius of the smaller circle \(AF=5\). Find the radius of the large circle.

Two circles with centres \(A\) and \(C\) are tangent to each other at the point \(B\). Two points \(D\) and \(E\) are chosen on the circles in such a way that a segment \(DE\) passes through the point \(B\). Prove that the tangent line to one circle at the point \(D\) is parallel to the tangent line to the other circle at the point \(E\).

The number \(n\) is natural. Show that: \[\frac1{\sqrt{1}} +\frac1{\sqrt{2}}+ \frac1{\sqrt{3}} + \dots +\frac1{\sqrt{n}} < 3 \sqrt{n+1} -3.\]

If \(n\) is a positive integer, we denote by \(s(n)\) the sum of the divisors of \(n\). For example, the divisors of \(n=6\) are \(1,2,3,6\), so \(s(6)=1+2+3+6=12\). Prove that, for all \(n\geq1\), \[s(1)+s(2)+\cdots+s(n)\leq n^2.\] Denote by \(t(n)\) is instead the sum of the squares of the divisors of \(n\) (e.g., \(t(6)=1^2+2^2+3^2+6^2=50\)), can you find a similar inequality for \(t(n)\)?

There are \(16\) cities in the kingdom. We would like to build roads between these cities so that one can get from any city to any other without passing through more than one city on the way. To save cost, we would like to have no more than four roads coming out of each city. Prove that such a system of roads is unfortunately impossible to build.

The marked angles are all \(45^{\circ}\). Show that the total green and blue areas are the same.

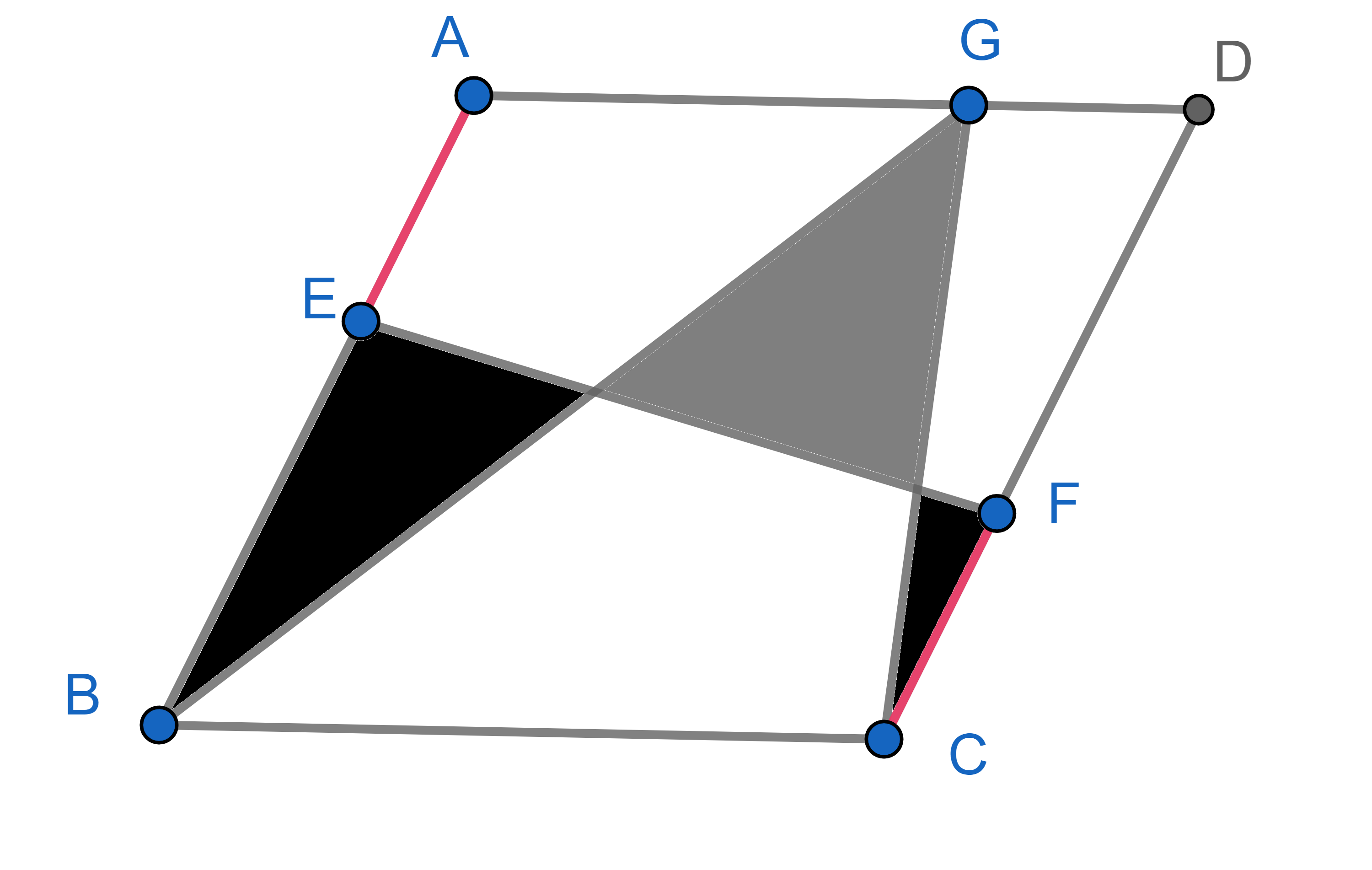
In a parallelogram \(ABCD\), point \(E\) belongs to the side \(AB\), point \(F\) belongs to the side \(CD\) and point \(G\) belongs to the side \(AD\). We know that the marked red segments \(AE\) and \(CF\) have equal lengths. Prove that the total grey area is equal to the total black area.