Problems

Jamie’s drawer is pretty big. It has infinitely many crayons. In fact, for every colour of crayon, there are infinitely many crayons of that colour.
In every group of \(9\) randomly chosen crayons from Jamie’s drawer, some \(3\) will have the same colour. Jamie chooses \(25\) crayons at random. Prove that some \(7\) of them will have the same colour.

Suppose \(n \ge 2\) cricket teams play in a tournament. No two teams play each other more than once, and no team plays itself. Prove that some two teams have to play the same number of games.

A rectangular parallelepiped of the size \(m\times n\times k\) is divided into unit cubes. How many rectangular parallelepipeds are formed in total (including the original one)?

Each integer on the number line is coloured either white or black. The numbers \(2016\) and \(2017\) are coloured differently. Prove that there are three identically coloured integers which sum to zero.

Detective Nero Wolf investigates a crime. He’s got \(80\) people involved in the case, among whom one is a criminal and another is a witness to the crime (but it is not known who either of them are). Each day the detective may invite one or more of these \(80\) people, and if there is a witness among those invited, but not the perpetrator, the witness will report who the perpetrator is. Can the detective solve a case in \(12\) days?

In the picture below you can see the graphs of \(K_5\), the complete graph on \(5\) vertices, and \(K_{3,3}\), the complete bipartite graph on \(3\) and \(3\) vertices. A theorem states that these graphs cannot be embedded into plane, namely one cannot draw graphs \(K_5\) and \(K_{3,3}\) on a plane in such a way that there are no intersecting edges.
The question is: can you draw the graphs \(K_5\) and \(K_{3,3}\) without intersecting edges on a torus?

In an \(n\times n\) table, two opposite corner squares are black and the rest are white. We wish to turn the whole \(n\times n\) table black in two stages. In the first stage, we paint black some of the squares that are white at the moment. In the second stage, we can perform the following two operations as much as we like. The row operation is to swap the colours of all the squares in a particular row. The column operation is to swap the colours of all the squares in a particular column. What is the fewest number of white squares that we can paint in the first stage?

An example of the row operation: let W stand for white and B stand for black and suppose that \(n=5\). Also suppose that a particular row has the colours WWBWB. Then performing the row operation would change this row to BBWBW.

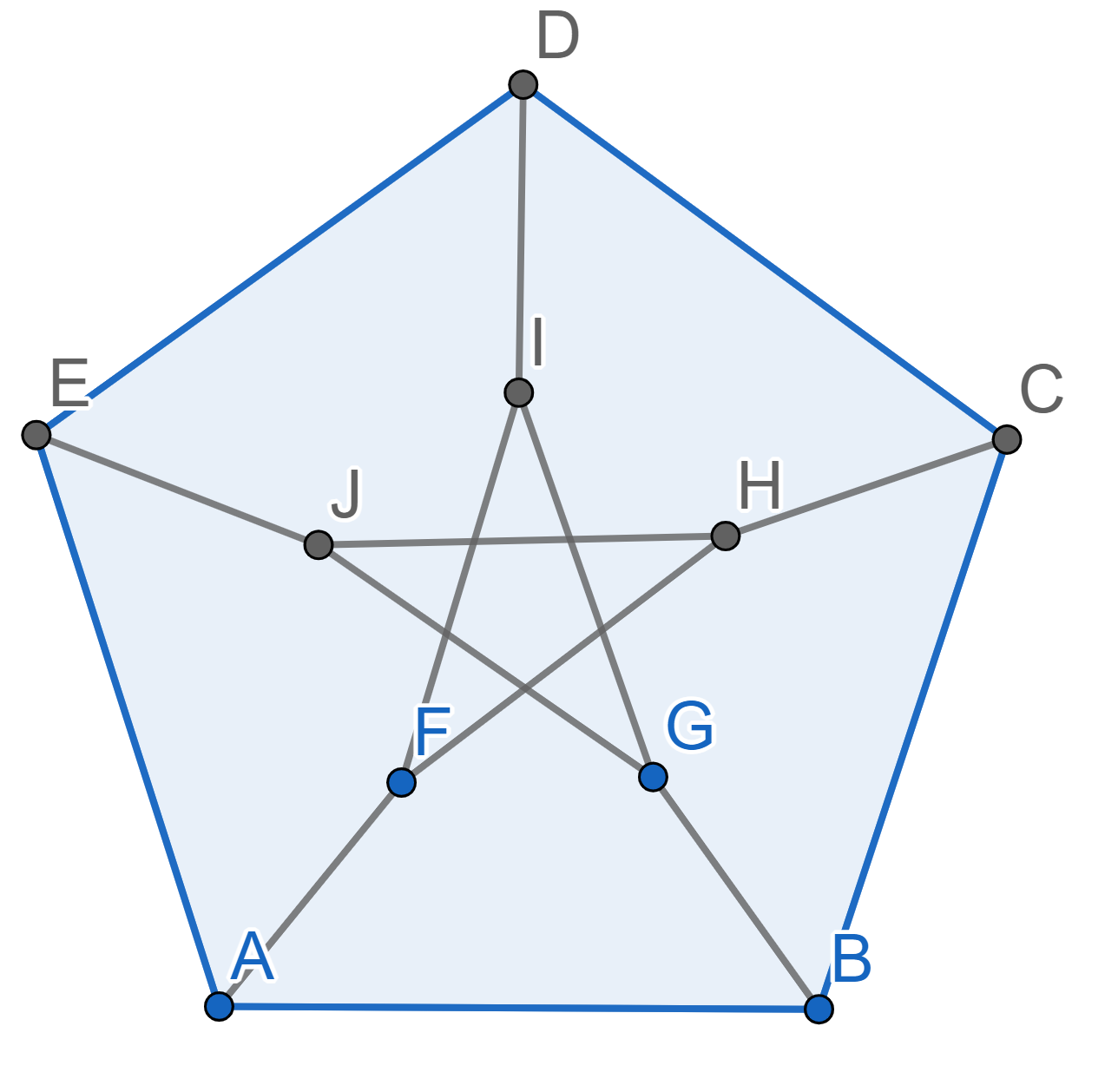
We want to color each of the 15 segments in the picture below using three colors. We need to color them so that if two segments share a point, then they are not the same color. For example, you cannot have both \(AB\) and \(BC\) be blue since they share the end \(B\). Is such a painting possible?

There is a scout group where some of the members know each other. Amongst any four members there is at least one of them who knows the other three. Prove that there is at least one member who knows the entirety of the scout group.

The distance between two villages equals \(999\) kilometres. When you go from one village to the other, every kilometre you see a sign on the road, saying \(0 \mid 999, \, 1\mid 998, \, 2\mid 997, ..., 999\mid 0\). The signs show the distances to the two villages. Find the number of signs that contain only two different digits. For example, the sign \(0\mid999\) contains only two digits, namely \(0\) and \(9\), whereas the sign \(1\mid998\) contains three digits, namely \(1\), \(8\) and \(9\).