Problems

On a \(10\times 10\) board, a bacterium sits in one of the cells. In one move, the bacterium shifts to a cell adjacent to the side (i.e. not diagonal) and divides into two bacteria (both remain in the same new cell). Then, again, one of the bacteria sitting on the board shifts to a new adjacent cell, either horizontally or vertically, and divides into two, and so on. Is it possible for there to be an equal number of bacteria in all cells after several such moves?

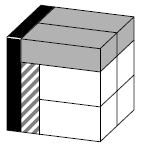
Michael made a cube with edge \(1\) out of eight bars as in the picture. All \(8\) bars have the same volume. The dimensions of the grey bars are the same as each other. Similarly, the dimensions of the white bars are the same as each other. Find the lengths of the edges of the white bars.

Red, blue and green chameleons live on an island. One day \(35\) chameleons stood in a circle. A minute later, they all changed colour at the same time, each changing into the colour of one of their neighbours. A minute later, everyone again changed their colours at the same time into the colour of one of their neighbours. Is it ever possible that each chameleon was each of the colours red, blue and green at some point? For example, it’s allowed for a chameleon to start off blue, turn green after one minute, then turn red after the second minute. It’s not allowed for a chameleon to start off blue, turn green after one minute, but then turn back to blue after the second minute.

Let \(a\), \(b\) and \(c\) be the three side lengths of a triangle. Does there exist a triangle with side lengths \(a+1\), \(b+1\) and \(c+1\)? Does it depend on what \(a\), \(b\) and \(c\) are?

There is a triangle with side lengths \(a\), \(b\) and \(c\). Can you form a triangle with side lengths \(\frac{a}{b}\), \(\frac{b}{c}\) and \(\frac{c}{a}\)? Does it depend on what \(a\), \(b\) and \(c\) are? Give a proof if it is always possible or never possible. Otherwise, construct examples to show the dependence on \(a\), \(b\) and \(c\).
Recall that a triangle can be drawn with side lengths \(x\), \(y\) and \(z\) if and only if \(x+y>z\), \(y+z>x\) and \(z+x>y\).

There is a triangle with side lengths \(a\), \(b\) and \(c\). Does there exist a triangle with side lengths \(|a-b|\), \(|b-c|\) and \(|c-a|\)? Does it depend on what \(a\), \(b\) and \(c\) are?
Recall that a triangle can be formed with side lengths \(x\), \(y\) and \(z\) if and only if all the inequalities \(x+y>z\), \(y+z>x\) and \(z+x>y\) hold.

There is a triangle with side lenghts \(a\), \(b\) and \(c\). Does there exist a triangle with sides of lengths \(a^2+bc\), \(b^2+ca\) and \(c^2+ab\)? Does it depend on the values of \(a\), \(b\) and \(c\)?

Could you meet a person inhabiting this planet who asks you “Am I a Goop?"

On this planet you meet a couple called Tom and Betty. You hear Tom ask someone: “Are Betty and I both Goops?"
What kind is Betty?

You learn that one of the aliens living on this planet is a wizard. You learnt that by overhearing a certain question being asked on the planet. What question could that have been?