Problems

Prove that the vertices of a planar graph can be coloured in (at most) six different colours such that every pair of vertices joined by an edge are of different colours.

Note: a graph is planar if it can be drawn in the plane with no edges crossing. For example, three houses, each of which is connected to three utilities, is not a planar graph.
You may find it useful to use the Euler characteristic: a planar graph with \(v\) vertices, \(e\) edges and \(f\) faces satisfies \(v-e+f=2\).

Paloma wrote digits from \(0\) to \(9\) in each of the \(9\) dots below, using each digit at most once. Since there are \(9\) dots and \(10\) digits, she must have missed one digit.

In the triangles, Paloma started writing either the three digits at the corners added together (the sum), or the three digits at the corners multiplied together (the product). She gave up before finishing the final two triangles.

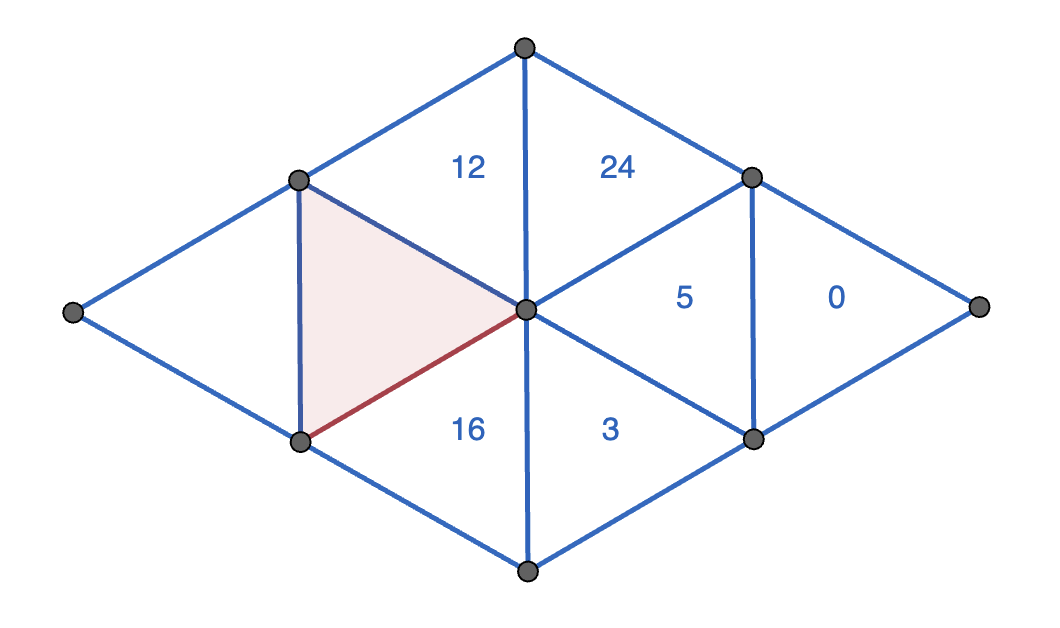
What numbers could Paloma have written in the interior of the red triangle? Demonstrate that you’ve found all of the possibilities.

How many subsets are there of \(\{1,2,...,10\}\) (the integers from \(1\) to \(10\) inclusive) containing no consecutive digits? That is, we do count \(\{1,3,6,8\}\) but do not count \(\{1,3,6,7\}\).
For example, when \(n=3\), we have \(8\) subsets overall but only \(5\) contain no consecutive integers. The \(8\) subsets are \(\varnothing\) (the empty set), \(\{1\}\), \(\{2\}\), \(\{3\}\), \(\{1,3\}\), \(\{1,2\}\), \(\{2,3\}\) and \(\{1,2,3\}\), but we exclude the final three of these.

The ant crawls a closed path along the edges of the dodecahedron, not turning back anywhere. The path runs exactly twice on each edge. Prove that the ant crawls on some edge of the dodecahedron in the same direction both times.

You have a deck of \(n\) distinct cards. Deal out \(k\) cards from the top one by one and put the rest of the deck on top of the \(k\) cards. What is the minimum number of times you need to repeat the action to return every card back to its position?

A simple polygon is a polygon that does not intersect itself and has no holes. Suppose we have a simple polygon \(S\) whose vertices consists of only integer coordinates.

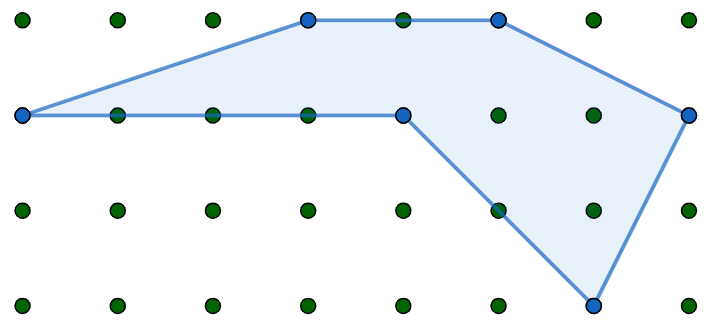
The area turns out to be remarkably easy to calculate. Count up the number of points with integer coordinate inside the polygon and on the boundary; call them \(i\) and \(b\) respectively. The area is then \[A(S) = i+\frac{b}{2}-1.\]

In the picture above, \(i=3\) and \(b=11\), so \(A(S) = \frac{15}{2}\). Prove that this formula for the area \(A(S)\) is correct.

For any positive integer \(k\), the factorial \(k!\) is defined as a product of all integers between 1 and \(k\) inclusive: \(k! = k \times (k-1) \times ... \times 1\). What’s the remainder when \(2025!+2024!+2023!+...+3!+2!+1!\) is divided by \(8\)?

You have in your possession a rotation of the sphere about an axis \(l\) through an angle \(\alpha\neq k\times360^{\circ}\) for any integer \(k\).

Consider the following funny rules. Suppose you have a rotation \(r_1\) through an angle \(\theta\) around an axis \(m\) and a rotation \(r_2\) through an angle \(\theta'\) around an axis \(m'\). You can add to your possession each of the below:

1. the rotation \(r_1^{-1}\) through \(-\theta\) around \(m\);

2. the rotation \(r_2r_1\) obtained by doing \(r_1\) and then \(r_2\);

3. the rotation \(g^{-1}r_1g\), where \(g\) is any rotation of the sphere.

Can you get all the rotations of the sphere?

Let us colour each side of a hexagon using one of yellow, blue or green. Any two configurations that can be rotated or reflected onto each other will be the same colouring for us. How many colourings are there?

Let \(u\) and \(v\) be two positive integers, with \(u>v\). Prove that a triangle with side lengths \(u^2-v^2\), \(2uv\) and \(u^2+v^2\) is right-angled.