Problems
Let \(\phi(n)\) be Euler’s function. Namely \(\phi(n)\) counts how many integers from \(1\) to \(n\) inclusive are coprime with \(n\). For two natural numbers \(m\), \(n\) such that \(\gcd(m,n)=1\), prove that \(\phi(mn) = \phi(m)\phi(n)\).
A natural number \(N\) is called perfect if it equals the sum of its divisors, except for \(N\) itself. Prove that if \(2^r-1\) is prime, then \((2^r-1)2^{r-1}\) is a perfect number. Are there any odd perfect numbers?
We want to prove Monsky’s theorem as a corollary of Sperner’s lemma:
it is not possible to dissect a square into an odd number of triangles
of equal area. After scaling we can consider the square with
coordinates: \((0,0),(0,1),(1,0),(1,1)\), which we want to
cut into \(n\) triangles with area
\(\frac{1}{n}\) each for an odd \(n\). Consider the following coloring of all
the points with rational coordinates \((\frac{p}{q},\frac{r}{s})\) inside the
square:
We look at the powers of \(2\) in the
fractions \((\frac{p}{q},\frac{r}{s})\), first of all
the numbers \(p,q\) are coprime, and
thus only one of them is divisible by \(2\), same with \(r,s\). Then the following possibilities
might occur:
Neither \(q\) nor \(s\) is divisible by \(2\). In this case we color the point red.
\(\frac{r}{s}\) is divisible by a larger or equal power of \(2\) than \(\frac{p}{q}\) and \(p\) is not divisible by \(2\). In this case we color the point blue.
\(\frac{p}{q}\) is divisible by a strictly larger power of \(2\) than \(\frac{r}{s}\) and \(r\) is not divisible by \(2\). In this case we color the point green.
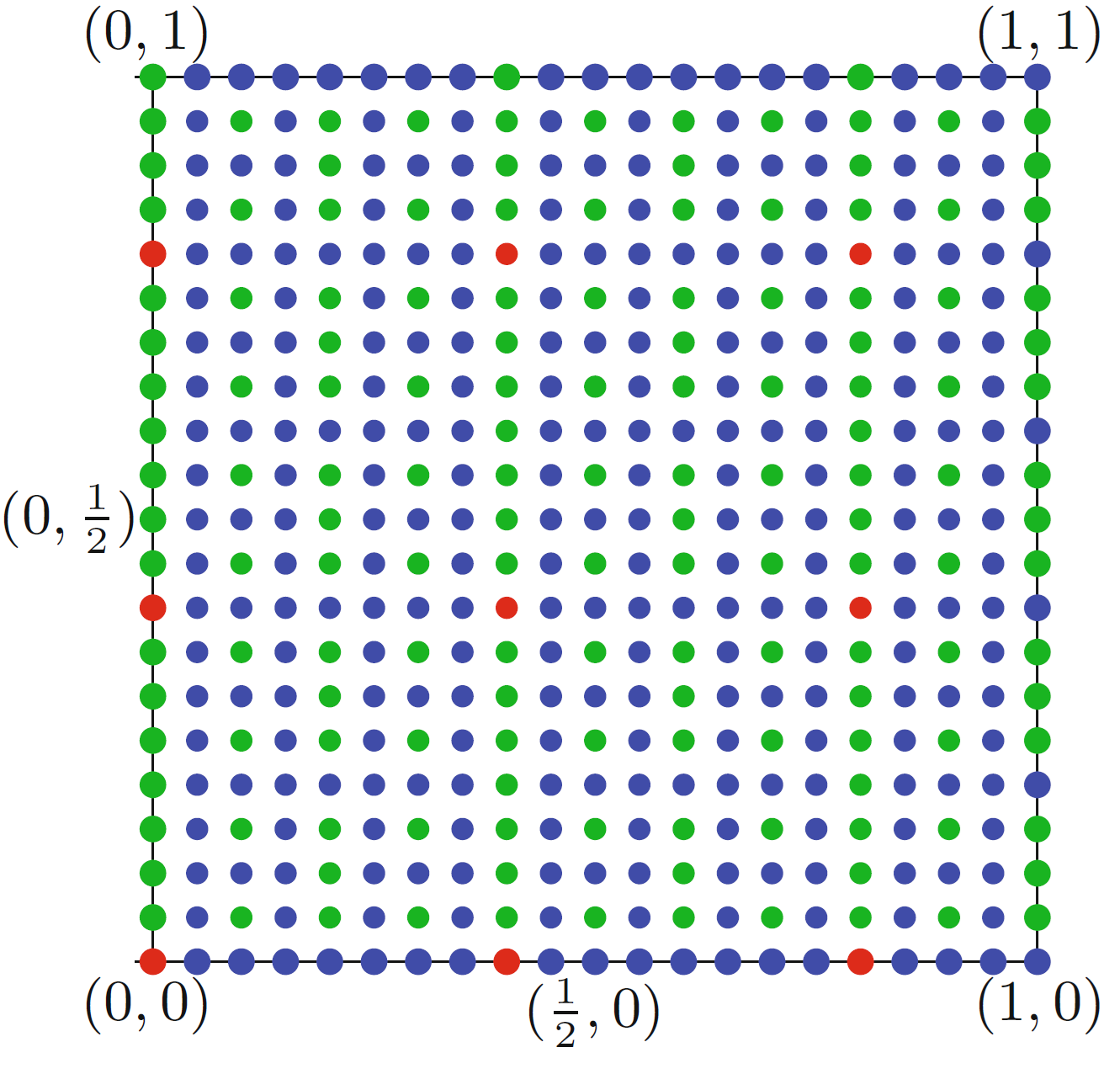
Under an assumption (which you do not have to prove) that the area of any rainbow triangle is at least \(\frac{1}{2}\) prove the Monsky’s theorem.
Without using any wolves, show that Robinson’s goat can only graze shapes that are convex (that means, whenever you pick two points inside the shape, the whole line between them also lies inside). But if Robinson is allowed to use as many wolves as he likes, this restriction disappears. Show that in this case, he can make the goat graze in the shape of any polygon at all.
In a field, there are two pegs, \(A\) and \(B\), placed \(15\) metres apart. Each peg has a small ring on top, and a rope can slide freely through these rings. You have one rope and two goats that want to graze the grass, but they will fight each other if they can both reach the same spot.
The rope may be arranged in any way you choose: it could pass through both rings, only one, or neither, depending on your setup. For what lengths of rope can you arrange things so that the goats cannot fight each other?
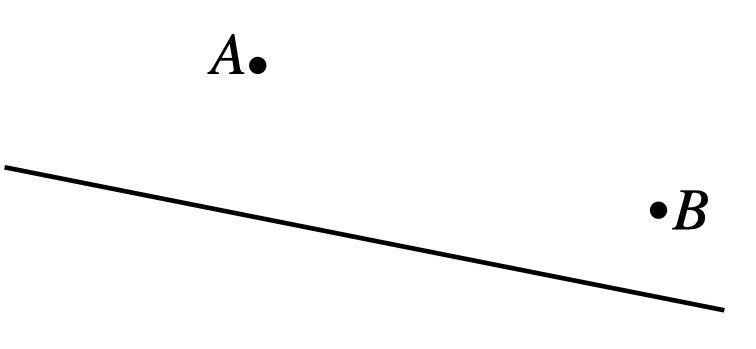
Fred starts running from point \(A\) and must reach point \(B\). On the way, he has to touch the fence shown as a straight line in the figure. It doesn’t matter where he touches the fence, as long as he does. What is the shortest path he can take?
Robbie and Paloma are playing football on a large, flat field. They both run at the same speed toward the ball. Where could the ball have been if Paloma reached it first?
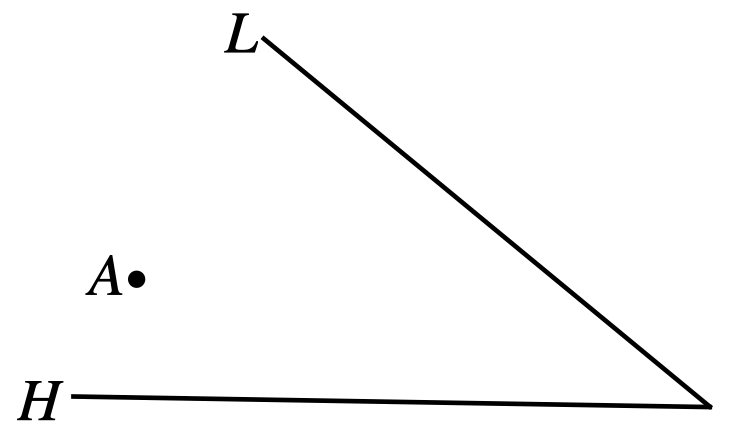
Oliver starts running from point \(A\) in the figure below. He must touch line \(H\), and then line \(L\). What is the shortest path he can take?
Two ants move along the same straight line and can only move back and forth along it. The first ant moves twice as fast as the second. Where could you place a breadcrumb so that the slower ant reaches it first?
Two ants, Muffy and Chip, start on opposite sides of a circle. Muffy moves twice as fast as Chip, and both can only move along the circle’s edge. Where could a breadcrumb be placed so that they both reach it at the same time?