Problems

The sequence \((a_n)\) is given by the conditions \(a_1 = 1000000\), \(a_{n + 1} = n \lfloor a_n/n\rfloor + n\). Prove that an infinite subsequence can be found within it, which is an arithmetic progression.

Given a square trinomial \(f (x) = x^2 + ax + b\). It is known that for any real \(x\) there exists a real number \(y\) such that \(f (y) = f (x) + y\). Find the greatest possible value of \(a\).

In the infinite sequence \((x_n)\), the first term \(x_1\) is a rational number greater than 1, and \(x_{n + 1} = x_n + \frac{1}{\lfloor x_n\rfloor }\) for all positive integers \(n\).

Prove that there is an integer in this sequence.

Note that in this problem, square brackets represent integers and curly brackets represent non-integer values or 0.

On the plane coordinate axes with the same but not stated scale and the graph of the function \(y = \sin x\), \(x\) \((0; \alpha)\) are given.

How can you construct a tangent to this graph at a given point using a compass and a ruler if: a) \(\alpha \in (\pi /2; \pi)\); b) \(\alpha \in (0; \pi /2)\)?

The sequence \(a_1, a_2, \dots\) is such that \(a_1 \in (1,2)\) and \(a_{k + 1} = a_k + \frac{k}{a_k}\) for any positive integer \(k\). Prove that it cannot contain more than one pair of terms with an integer sum.The sequence \(a_1, a_2, \dots\) is such that \(a_1 \in (1,2)\) and \(a_{k + 1} = a_k + \frac{k}{a_k}\) for any positive integer \(k\). Prove that it cannot contain more than one pair of terms with an integer sum.

Prove that if the expression

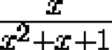
takes a rational value, then the expression

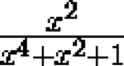
also takes on a rational value.

Which numbers can stand in place of the letters in the equality \(AB \times C = DE\), if different letters denote different numbers and from left to right the numbers are written in ascending order?

Prove that if the numbers \(x, y, z\) satisfy the following system of equations for some values of \(p\) and \(q\): \[\begin{aligned} y &= x^2 + px + q,\\ z &= y^2 + py + q,\\ x &= z^2 + pz + q, \end{aligned}\] then the inequality \(x^2y + y^2z + z^2x \geq x^2z + y^2x + z^2y\) is satisfied.

There are 40 weights of weights of 1 g, 2 g, ..., 40 grams. Of these, 10 weights of even weight were chosen and placed on the left hand side of the scales. Then we selected 10 weights of odd weight and put it on the right hand side of the scales. The scales were balanced. Prove that on one of the bowls of the scales there are two weights with a mass difference of 20 g.

Mark has 1000 identical cubes, each of which has one pair of opposite faces which are coloured white, another pair which are blue and a third pair that are red. He made a large \(10 \times 10 \times 10\) cube from them, joining cubes to one another which have the same coloured faces. Prove that the large cube has a face which is solidly one colour.