Problems
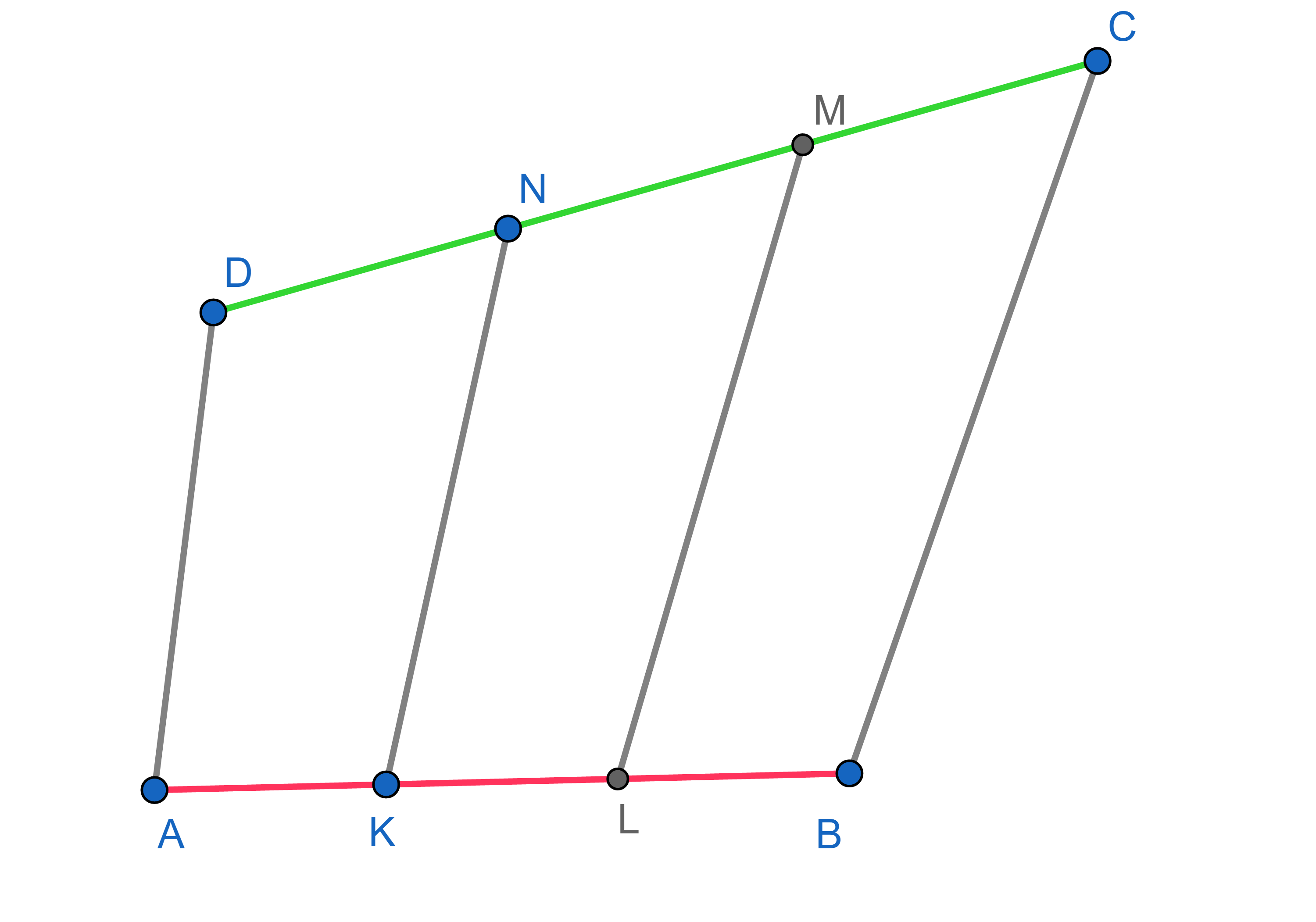
A quadrilateral \(ABCD\) is given. Points \(K\) and \(L\) belong to the side \(AB\) and \(AK=KL=LB\) and points \(N\) and \(M\) belong to the side \(CD\) and \(CM=MN=ND\). Show that the area of the quadrilateral \(KLMN\) is \(\frac13\) of the area of the quadrilateral \(ABCD\).
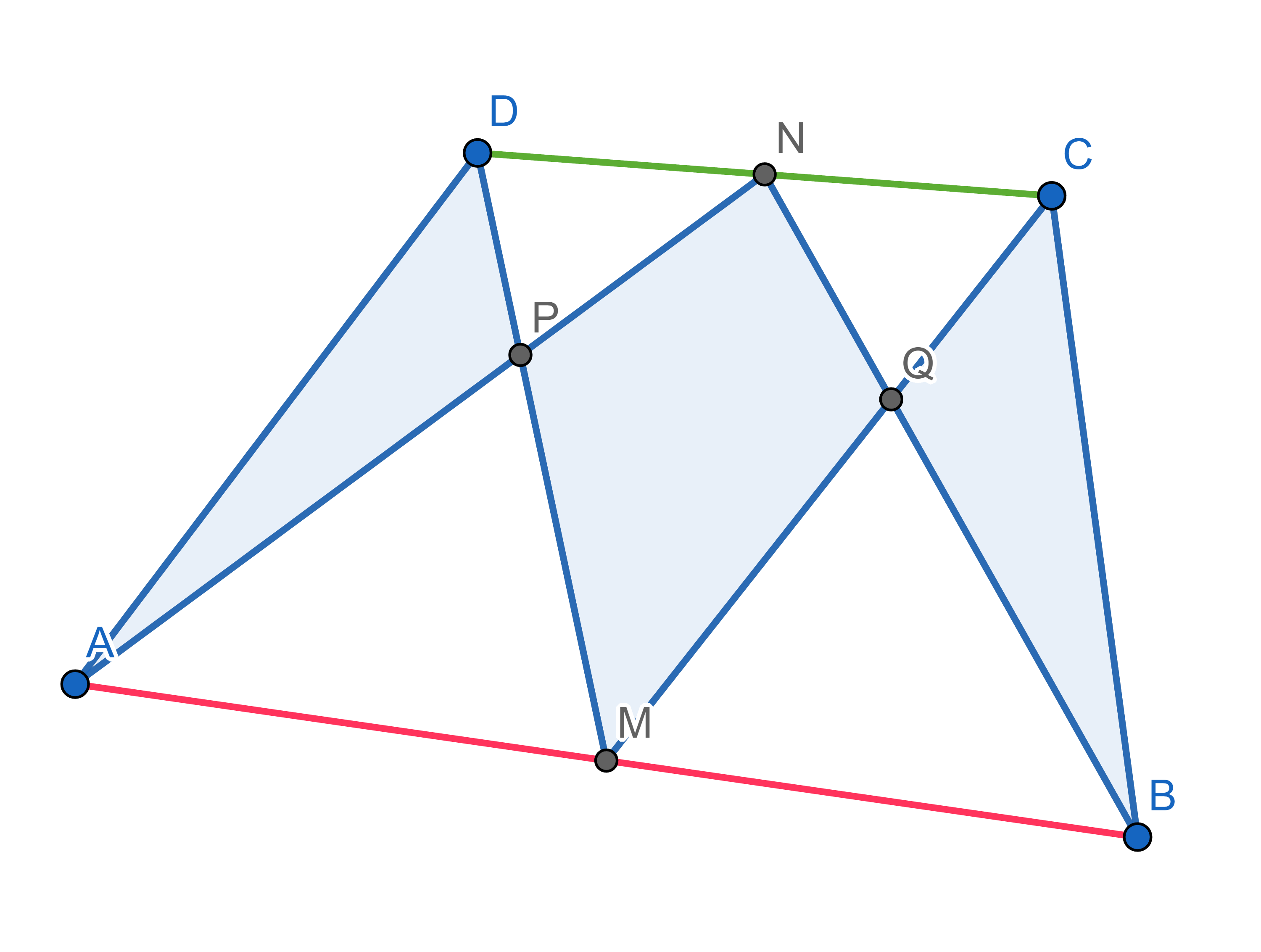
A quadrilateral \(ABCD\) is given. Point \(M\) is a midpoint of \(AB\) and point \(N\) is a midpoint of \(CD\). Point \(P\) is where segments \(AN\) and \(DM\) meet, point \(Q\) is where segments \(MC\) and \(NB\) meet. Show that the sum of the areas of triangles \(APD\) and \(BCQ\) is equal to the area of the quadrilateral \(MQNP\).
The marked angles are all \(45^{\circ}\). Show that the total green and blue areas are the same.
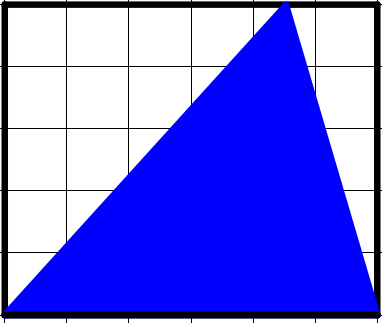
Each of the small squares has an area of \(1\). What is the area of the triangle?
Each number denotes the area of the rectangle it is written into. What number should be written where the “?" character is?

Each number denotes the area of the rectangle it is written into. What number should be written where the "?" character is?

A square was cut with two parallel lines. The perpendicular distance between these two lines is \(6\)cm. One of them goes through the top right corner and the other through the bottom left corner. The three regions obtained this way, two triangles and a parallelogram, have equal areas. What is the area of the square?

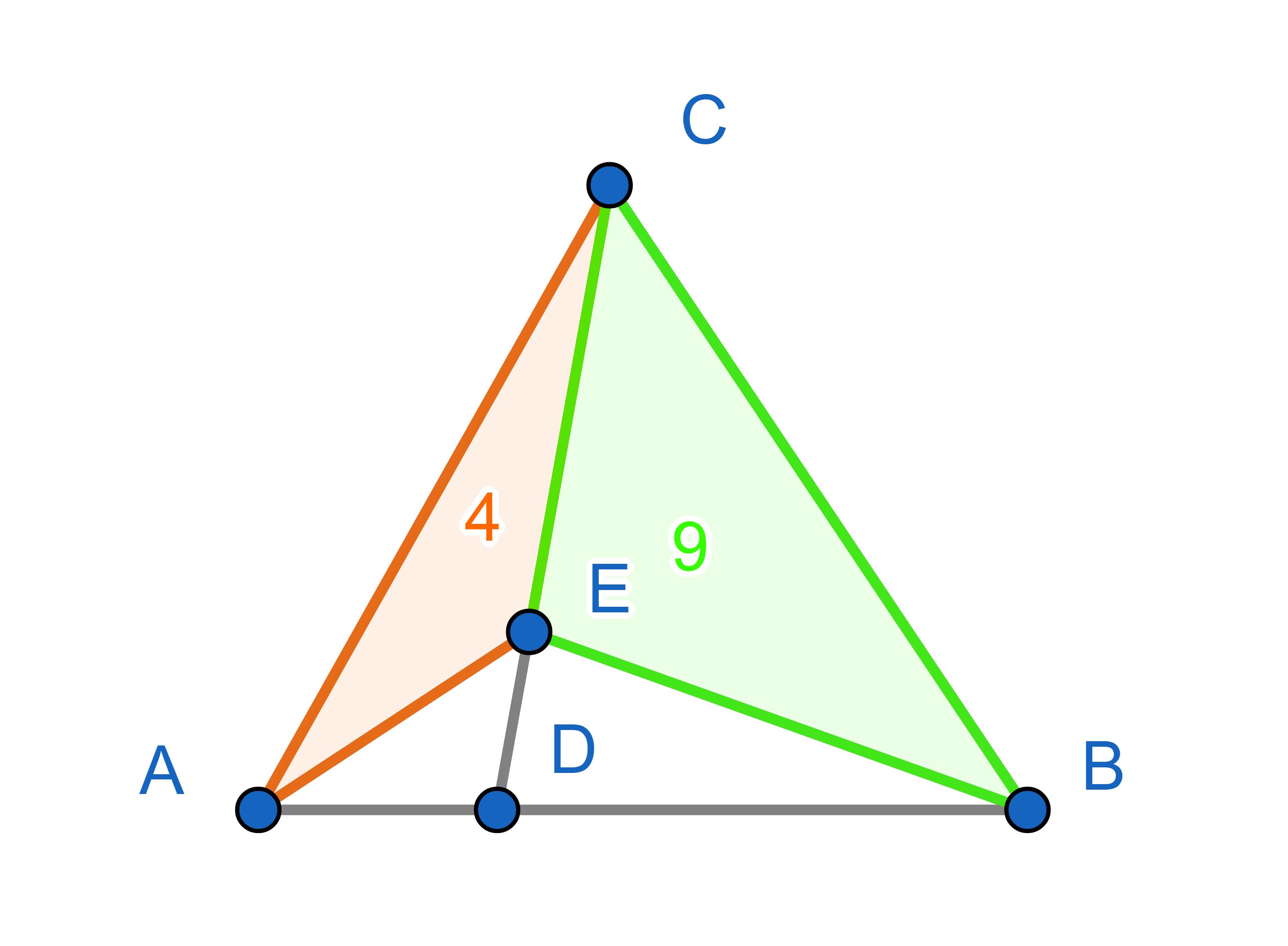
The area of the triangle \(\triangle AEC\) is \(4\), the area of the triangle \(\triangle BCE\) is \(9\) and the area of the triangle \(\triangle ABC\) is \(21\). What is the area of the triangle \(\triangle ADE\)?
A series of squares are connected by touching vertices. Some triangles were drawn outside and inside of the chain. Show that the total green area is the same as the total red area.
In a triangle \(\triangle ABC\), \(D\) is the midpoint of \(BC\), and \(E\) is the midpoint of \(AD\). \(F\) is the intersection of the side \(AC\) with \(BE\). What is the area of the triangle \(\triangle AEF\) as a proportion of the area of the triangle \(\triangle ABC\)?