Problems
After some playing with the \(3\times 3\) board, Sam guessed that there were \(900\) different light patterns that could be obtained by playing on this board. Was he right?
The original “Lights Out” game works like this: a light pattern is shown on the board, and your task is to turn all the lights off. A light pattern is called solvable if you can complete the game starting from that pattern. Ziheng and Jan are playing on an \(n\times n\) board, and they notice that some patterns are unsolvable. Can you find a rule to decide when a pattern is not solvable?
A rectangle has a perimeter of \(1\). Is it possible that its area is larger than \(1000\)?
Zahra has a \(3\times 3\) grid of little squares. Can she write the numbers \(2,4,6,7,8,10,12,14,16\) inside the little square - using each number exactly once - so that the sum of the three numbers in every row is the same?
When Robinson Crusoe was stranded on his island, he found a goat and decided to keep it. To stop the goat from running away, he tied it to a peg in the ground with a rope. The goat wandered around happily, eating all the grass it could reach until the rope pulled tight. For example, Robinson noticed that with just one peg and one rope of length \(5\) meters, the grazed area was exactly a circle of radius \(5\) meters!
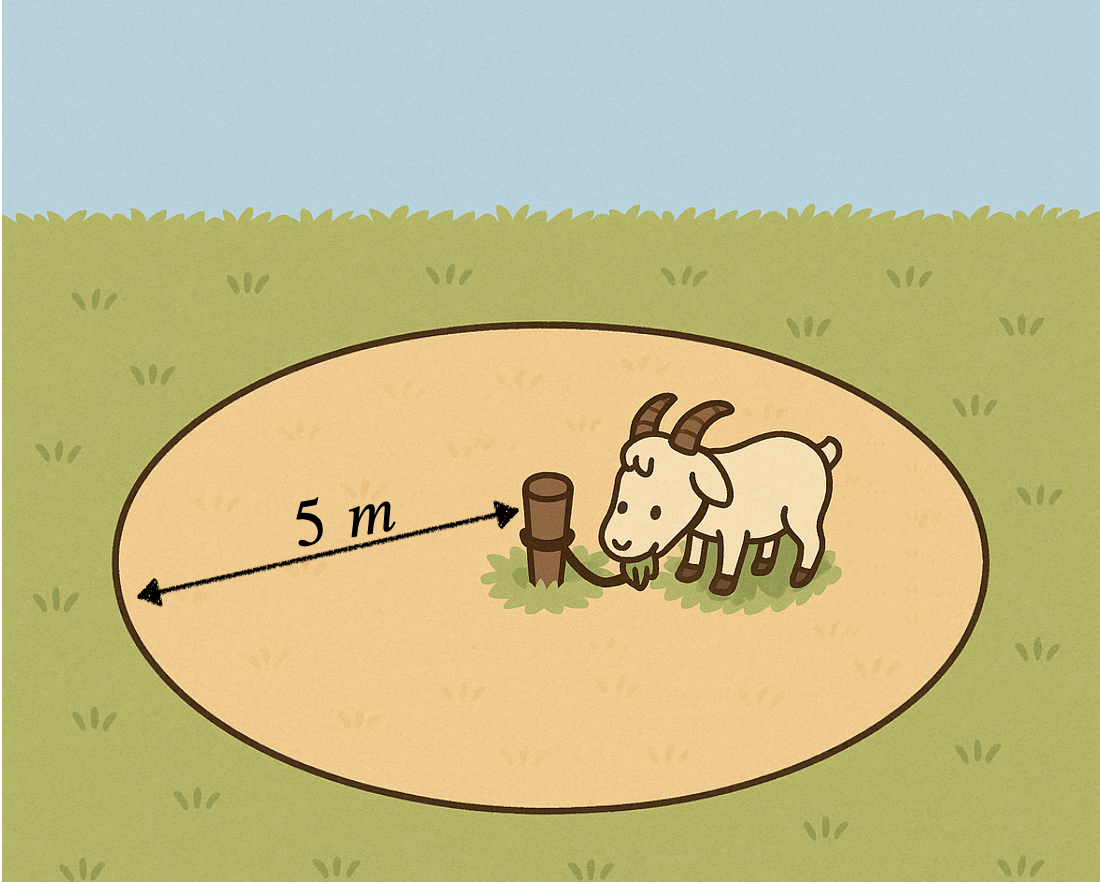
In this sheet we will explore what shapes the goat can graze when Robinson uses pegs, ropes, and even small sliding rings in slightly more complicated positions. In mathematics, the shape made by all points that satisfy a condition is called a locus (plural: loci). In our problems, the locus of the goat is the area it can graze. Before we begin, here are the rules of the game:
We will treat the goat as a single point, and the rope as a fixed length that cannot stretch, so the goat can graze any point it can reach before the rope is tight. A peg is simply a point in the ground that does not move. Let’s see some more interesting examples:
Welcome everybody! In today’s session we will be talking about divisibility tricks. Recall that a number \(a\) is divisible by another number \(b\) if \(a\) divided by \(b\) is a whole number. Often, there are quick ways to check divisibility without doing the full division. For example, a number is divisible by \(5\) if and only if its last digit is \(0\) or \(5\). It is important to remember that this phrase “if and only if" actually means two things:
If a number is divisible by \(5\), then its last digit must be \(0\) or \(5\).
If a number’s last digit is \(0\) or \(5\), then the number is divisible by \(5\).
It is useful to think about this in terms of there being two directions. In today’s sheet we will see many more such tricks, and remember: usually you will need to prove both directions!
Long before meeting Snow White, the seven dwarves lived in seven different mines. There is an underground tunnel connecting any two mines. All tunnels were separate, so you could not start in one tunnel and somehow end up in another. Is it possible to walk through every tunnel exactly once without retracing your path?
There is a queue of \(n\) truth tellers and liars. The first person says, “more than half of us are liars". The second person says, “more than a quarter of us are liars". The third person says, “more than an eighth of us are liars", and so on, until the \(n\)th person says, “more than \(\frac{1}{2^n}\) of us are liars". Describe what the number of truth-tellers and liars could be, as well as their placement in the queue. Note that the solutions are not fixed numbers.
Sam was playing on the \(3\times 3\) lights out board, and starting from all lights off, he pressed every single button on the board. What light pattern did he get in the end?
Find a quiet plan for the \(1\times 5\) “Lights Out" board.