Problems

Two semicircles and one circle were drawn on the sides of a right triangle. The circle whose centre is in the midpoint of the hypothenuse actually goes through the right angle corner – this is a general fact, but you don’t need to prove it here. If the two shorter sides of the triangle are \(3\) and \(4\), what is the total area of the red region?

The lengths of three sides of a right-angled triangle are all integers.

Show that one of them is divisible by \(3\).

A segment \(AB\) is a base of an isosceles triangle \(ABC\). A line perpendicular to the segment \(AC\) was drawn through point \(A\) – this line crosses an extension of the segment \(BC\) at point \(D\). There is also a point \(E\) somewhere, such that angles \(\angle ECB\) and \(\angle EBA\) are both right angles. Point \(F\) is on the extension of the segment \(AB\), such that \(B\) is between \(A\) and \(F\). We also know that \(|BF|=|AD|\). Show that \(|ED|=|EF|\).

Prove that the area \(S_{ABC}\) of a triangle is equal to \(abc/4R\).

The point \(D\) lies on the base \(AC\) of the isosceles triangle \(ABC\). Prove that the radii of the circumscribed circles of the triangles \(ABD\) and \(CBD\) are equal.

Express the area of the triangle \(ABC\) through the length of the side \(BC\) and the angles \(B\) and \(C\).

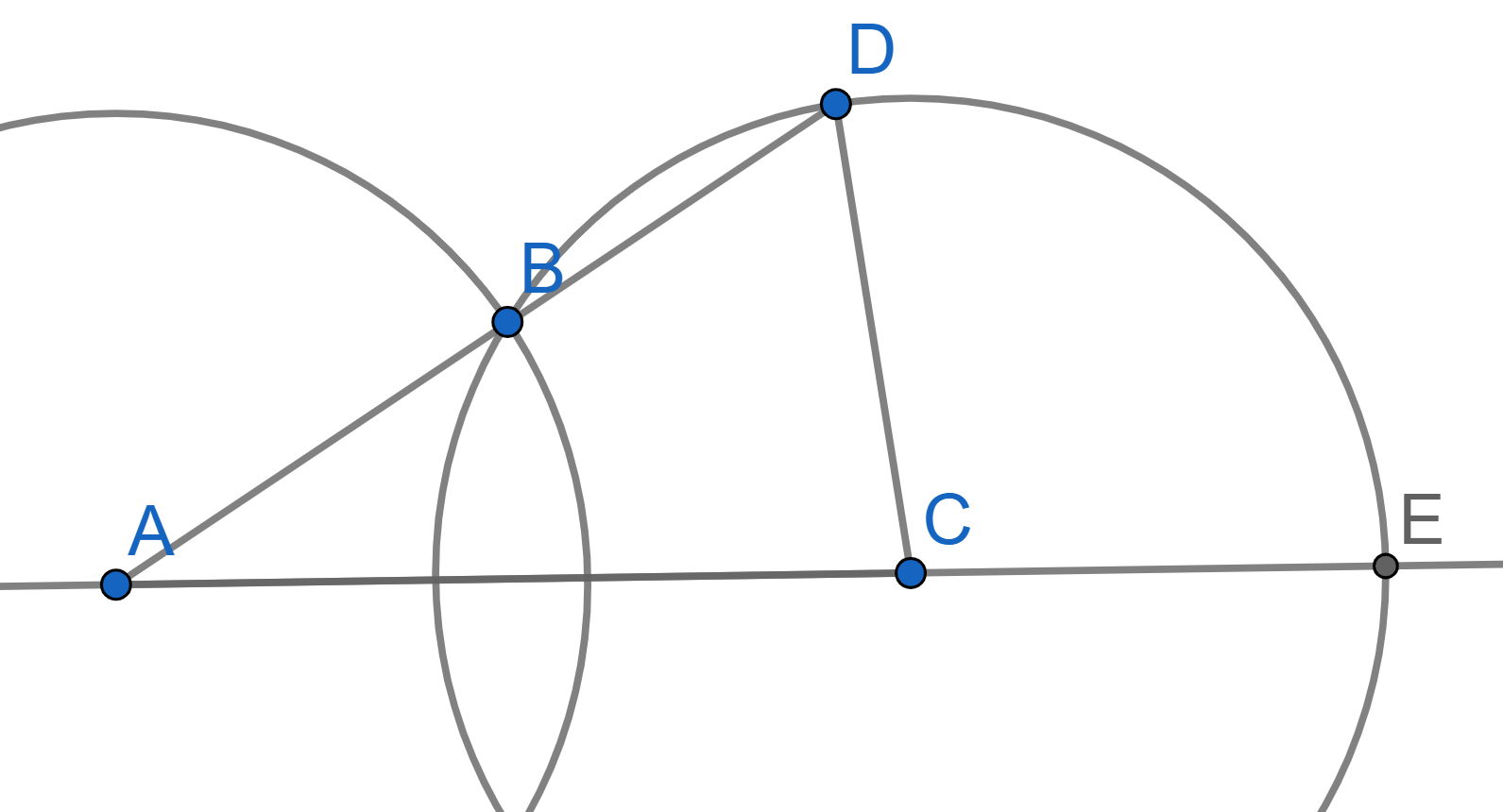
Two intersecting circles of radius \(R\) are given, and the distance between their centers is greater than \(R\). Prove that \(\angle ECD = 3\angle CAD\).

Find all triangles in which the angles form an arithmetic progression, and the sides form: a) an arithmetic progression; b) a geometric progression.

There are 5 points inside an equilateral triangle with side of length 1. Prove that the distance between some two of them is less than 0.5.

A unit square is divided into \(n\) triangles. Prove that one of the triangles can be used to completely cover a square with side length \(\frac{1}{n}\).