Problems

Let \(AA_1\) and \(BB_1\) be the heights of the triangle \(ABC\). Prove that the triangles \(A_1B_1C\) and \(ABC\) are similar.

Let \(G,F,H\) and \(I\) be the midpoints of the sides \(CD, DA, AB, BC\) of the square \(ABCD\), whose area is equal to \(S\). Find the area of the quadrilateral formed by the straight lines \(BG,DH,AF,CE\).

a) Prove that if in the triangle the median coincides with the height then this triangle is an isosceles triangle.

b) Prove that if in a triangle the bisector coincides with the height then this triangle is an isosceles triangle.

Prove that the bisectors of a triangle intersect at one point.

A circle divides each side of a triangle into three equal parts. Prove that this triangle is regular.

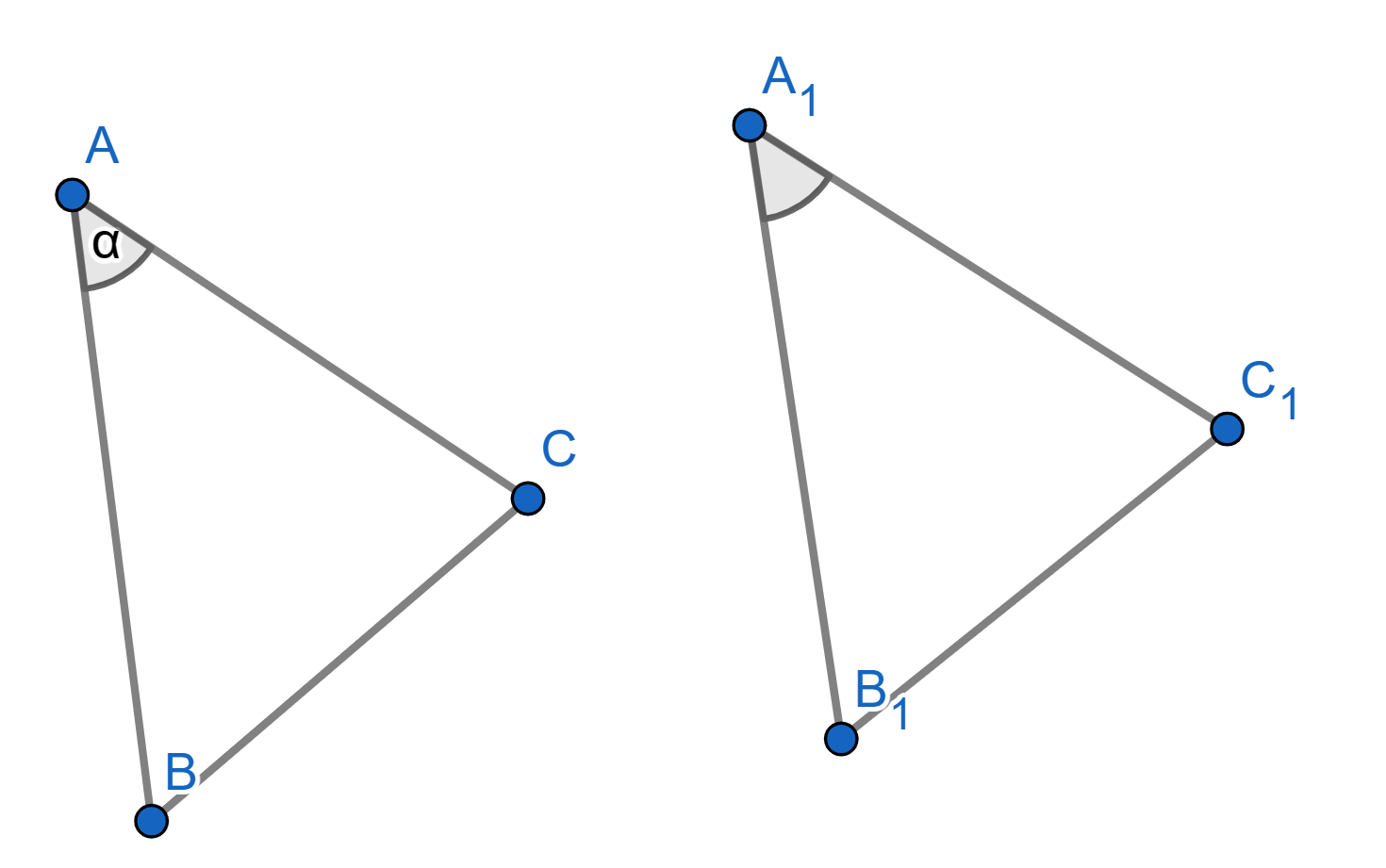
Let \(ABC\) and \(A_1B_1C_1\) be two triangles with the following properties: \(AB = A_1B_1\), \(AC = A_1C_1\), and angles \(\angle BAC = \angle B_1A_1C_1\). Then the triangles \(ABC\) and \(A_1B_1C_1\) are congruent. This is usually known as the “side-angle-side" criterion for congruence.

In the triangle \(\triangle ABC\) the sides \(AC\) and \(BC\) are equal. Prove that the angles \(\angle CAB\) and \(\angle CBA\) are equal.

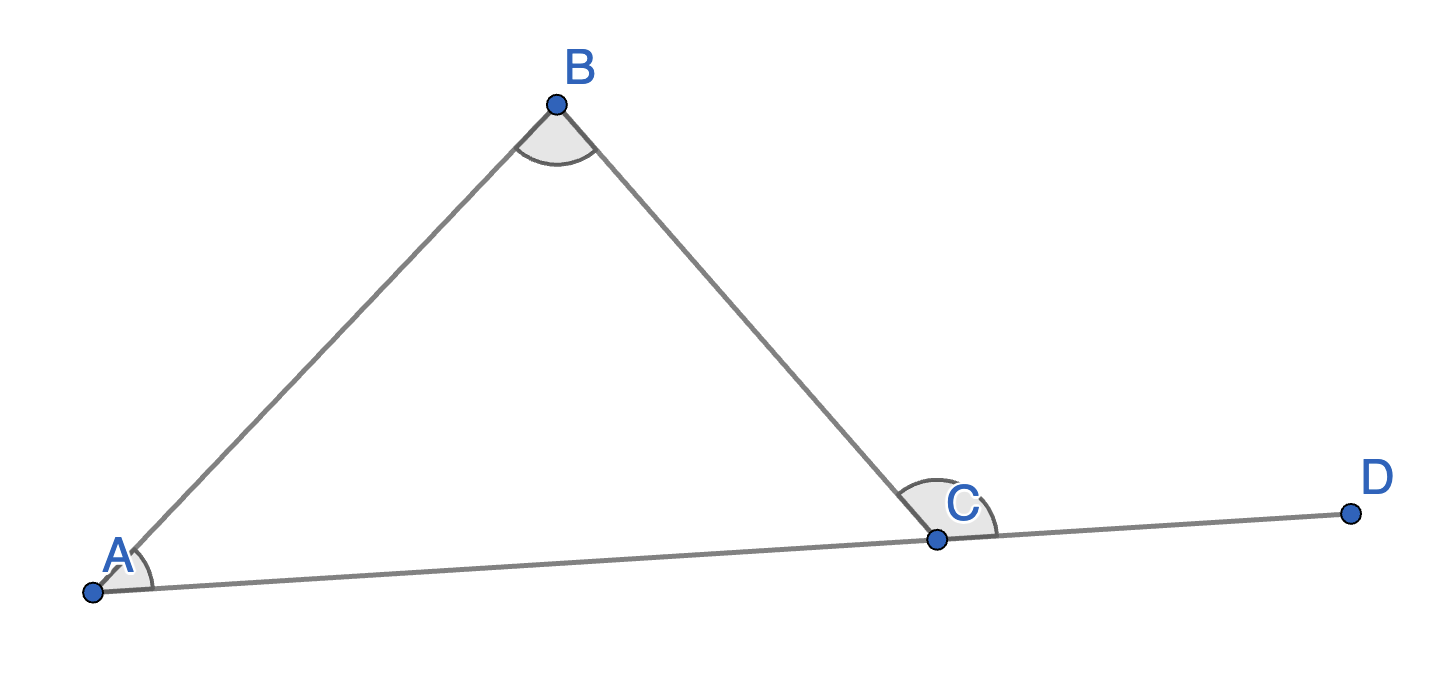
Let \(ABC\) be a triangle with given angles \(\angle BAC\) and \(\angle ABC\). What is the value of the angle \(\angle BCD\) in terms of \(\angle BAC\) and \(\angle ABC\)?

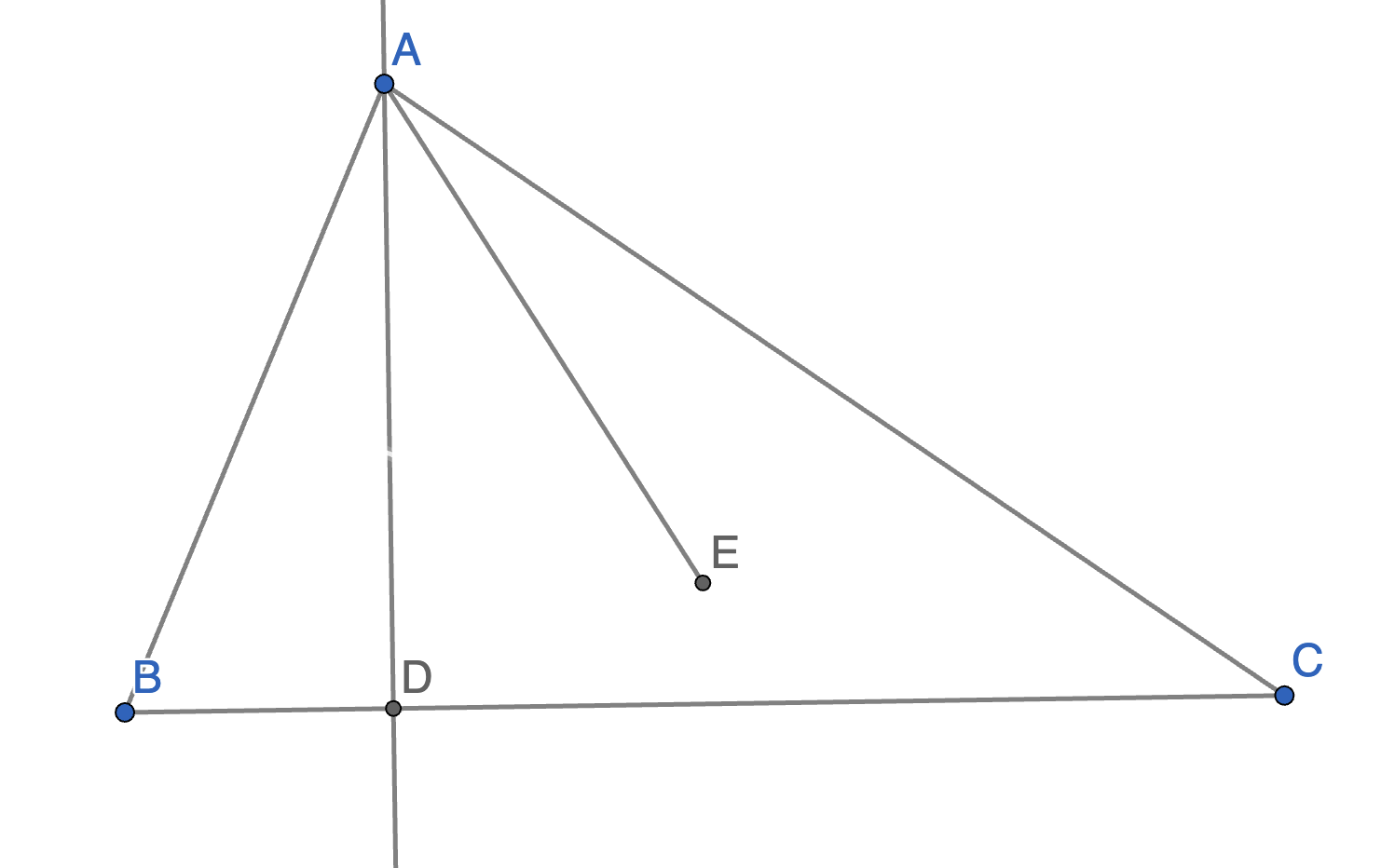
The triangle \(ABC\) is inscribed into the circle with centre \(E\), the line \(AD\) is perpendicular to \(BC\). Prove that the angles \(\angle BAD\) and \(\angle CAE\) are equal.

Let \(\triangle ABC\) and \(\triangle DEF\) be triangles such that the following angles are equal: \(\angle ABC = \angle DEF\) and \(\angle ACB = \angle DFE\). Prove that \(\triangle ABC\) and \(\triangle DEF\) are similar triangles.