Problems
In the infinite sequence \((x_n)\), the first term \(x_1\) is a rational number greater than 1, and \(x_{n + 1} = x_n + \frac{1}{\lfloor x_n\rfloor }\) for all positive integers \(n\).
Prove that there is an integer in this sequence.
Note that in this problem, square brackets represent integers and curly brackets represent non-integer values or 0.
On the plane coordinate axes with the same but not stated scale and the graph of the function \(y = \sin x\), \(x\) \((0; \alpha)\) are given.
How can you construct a tangent to this graph at a given point using a compass and a ruler if: a) \(\alpha \in (\pi /2; \pi)\); b) \(\alpha \in (0; \pi /2)\)?
The sequence \(a_1, a_2, \dots\) is such that \(a_1 \in (1,2)\) and \(a_{k + 1} = a_k + \frac{k}{a_k}\) for any positive integer \(k\). Prove that it cannot contain more than one pair of terms with an integer sum.The sequence \(a_1, a_2, \dots\) is such that \(a_1 \in (1,2)\) and \(a_{k + 1} = a_k + \frac{k}{a_k}\) for any positive integer \(k\). Prove that it cannot contain more than one pair of terms with an integer sum.
Prove that if the expression
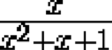
takes a rational value, then the expression
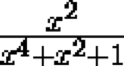
also takes on a rational value.
The nonzero numbers \(a\), \(b\), \(c\) are such that every two of the three equations \(ax^{11} + bx^4 + c = 0\), \(bx^{11} + cx^4 + a = 0\), \(cx^{11} + ax^4 + b = 0\) have a common root. Prove that all three equations have a common root.
The teacher wrote on the board in alphabetical order all possible \(2^n\) words consisting of \(n\) letters A or B. Then he replaced each word with a product of \(n\) factors, correcting each letter A by \(x\), and each letter B by \((1 - x)\), and added several of the first of these polynomials in \(x\). Prove that the resulting polynomial is either a constant or increasing function in \(x\) on the interval \([0, 1]\).
Prove that a graph with \(n\) vertices, the degree of each of which is at least \(\frac{n-1}{2}\), is connected.
In the Far East, the only type of transport is a carpet-plane. From the capital there are 21 carpet-planes, from the city of Dalny there is one carpet-plane, and from all of the other cities there are 20. Prove that you can fly from the capital to Dalny (possibly with interchanges).
a) they have 10 vertices, the degree of each of which is equal to 9?
b) they have 8 vertices, the degree of each of which is equal to 3?
c) are they connected, without cycles and contain 6 edges?
On the plane 100 circles are given, which make up a connected figure (that is, not falling apart into pieces). Prove that this figure can be drawn without taking the pencil off of the paper and going over any line twice.