Problems

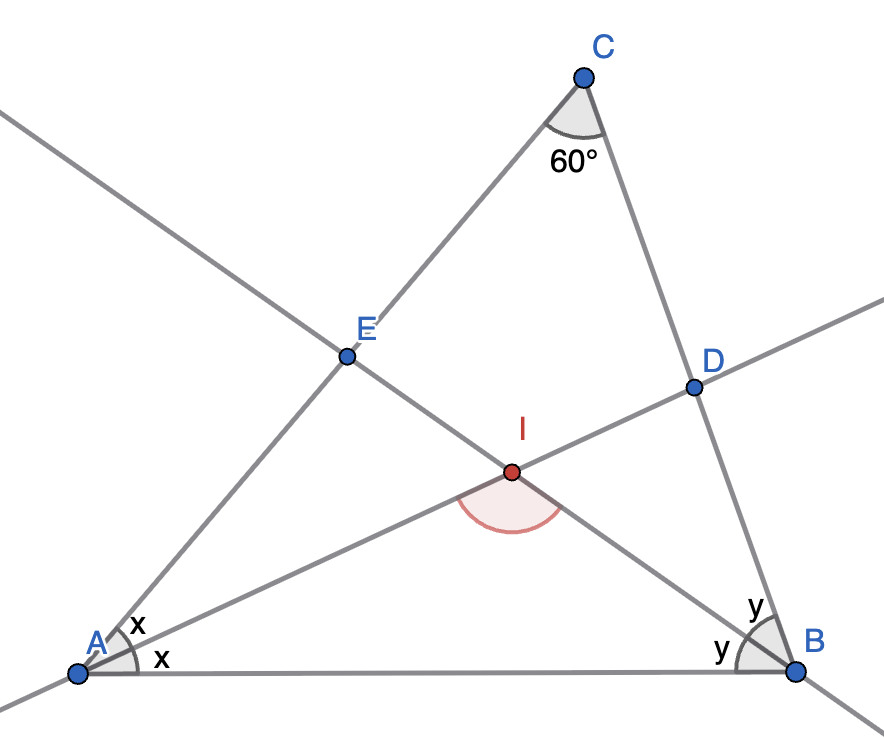
In the triangle \(\triangle ABC\), the angle \(\angle ACB=60^{\circ}\), marked at the top. The angle bisectors \(AD\) and \(BE\) intersect at the point \(I\).

Find the angle \(\angle AIB\), marked in red.

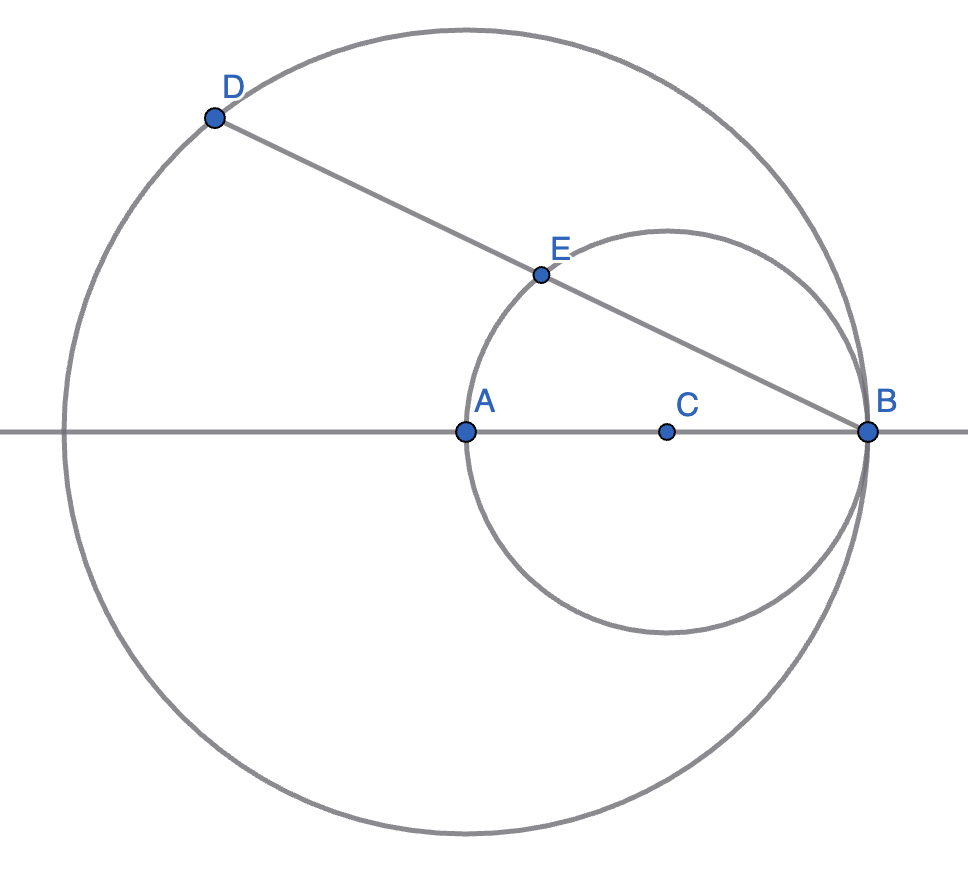
A circle with centre \(A\) has the point \(B\) on its circumference. A smaller circle is drawn inside this with \(AB\) as a diameter and \(C\) as its centre. A point \(D\) (which is not \(B\)) is chosen on the circumference of the bigger circle, and the line \(BD\) is drawn. \(E\) is the point where the line \(BD\) intersects the smaller circle.

Show that \(|BE|=|DE|\).

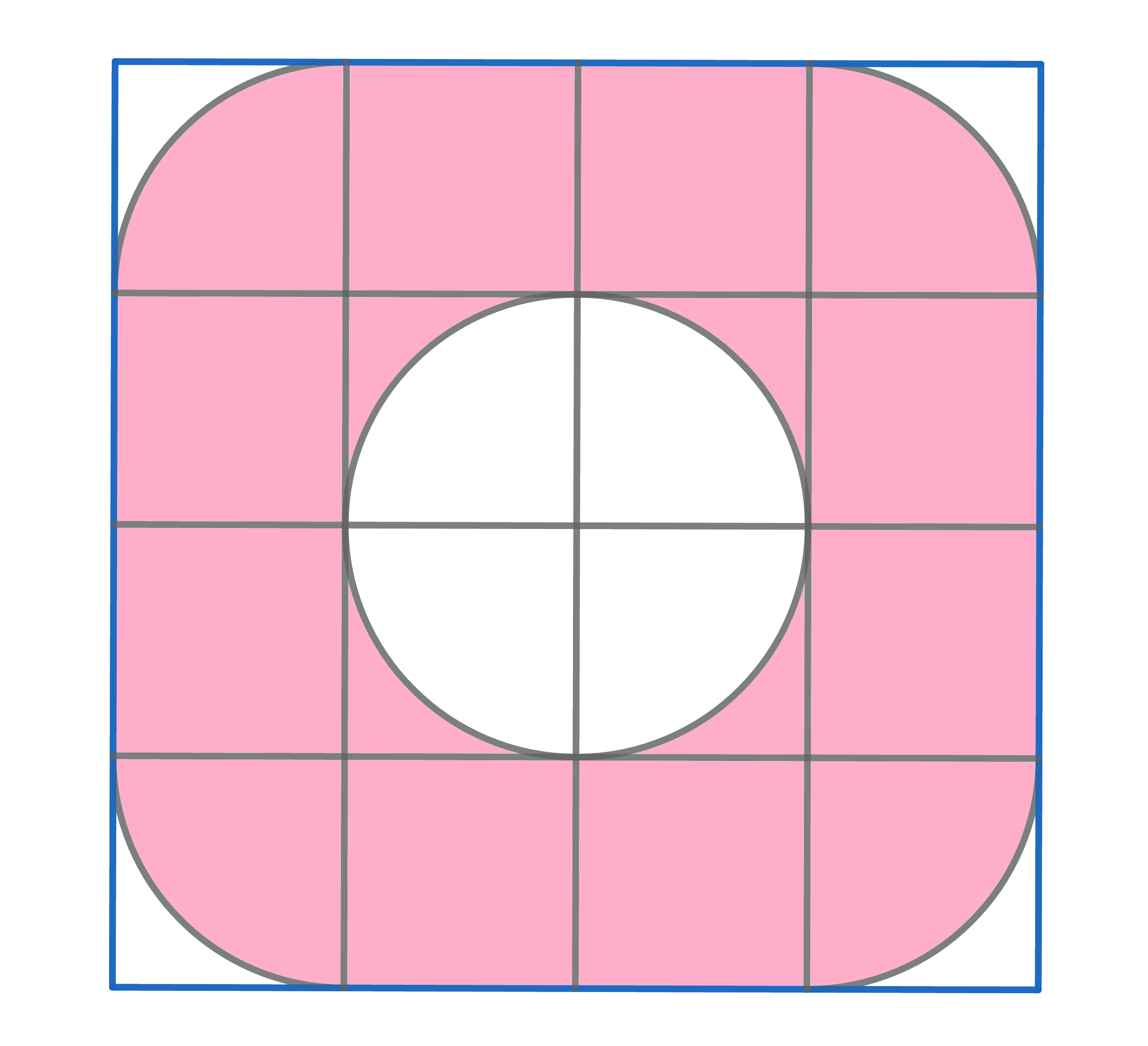
The area of the coloured figure equals \(48\)cm\(^2\). Find the length of the side of the smallest square.

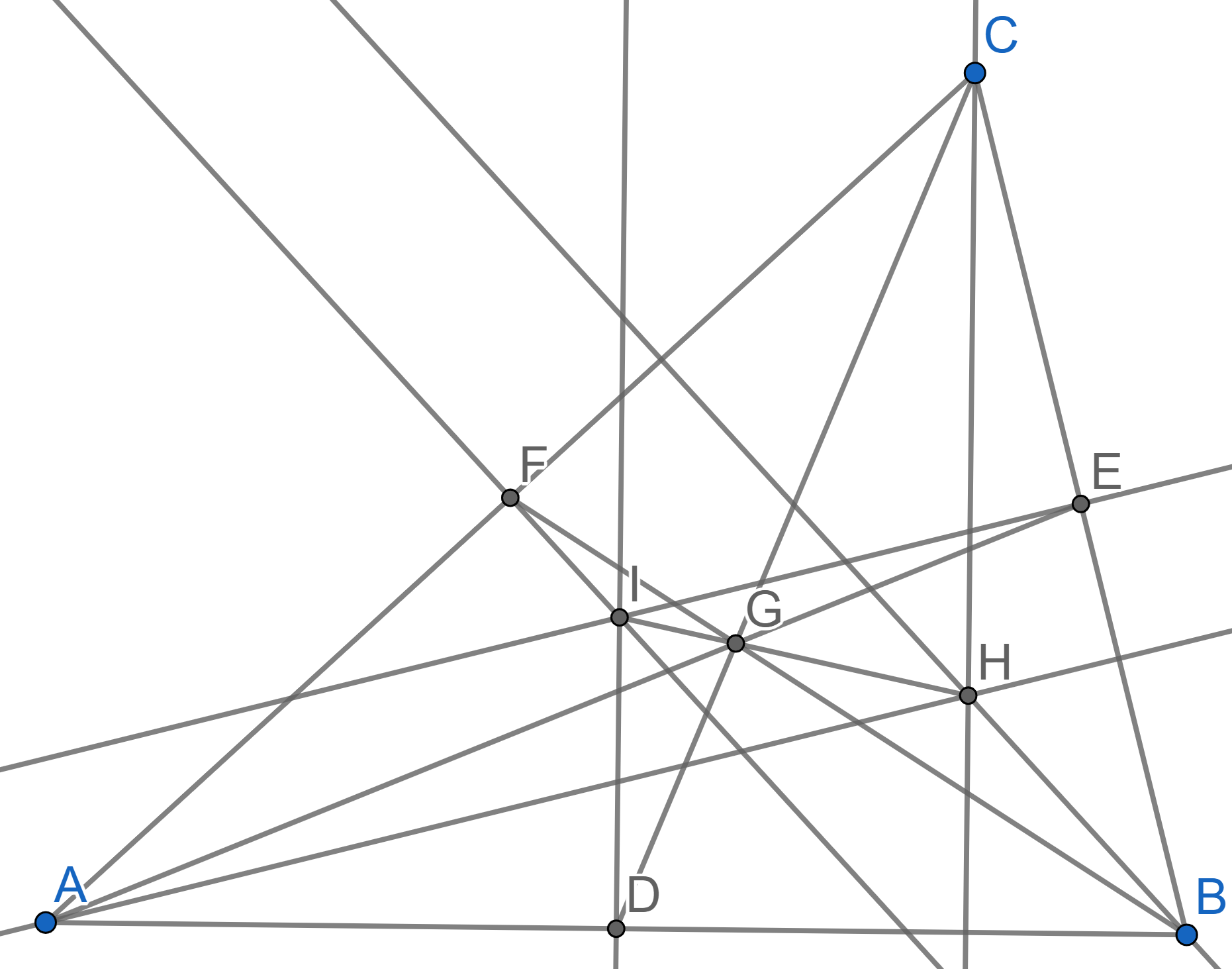
Let \(ABC\) be a non-isosceles triangle. The point \(G\) is the point of intersection of the medians \(AE\), \(BF\), \(CD\). The point \(H\) is the point of intersection of all heights. The point \(I\) is the center of the circumscribed circle of \(ABC\), or the point of intersection of all perpendicular bisectors to the segments \(AB\), \(BC\), \(AC\).
Prove that points \(I,G,H\) lie on one line and that the ratio \(IG:GH = 1:2\). The line that all of \(I\), \(G\) and \(H\) lie on is called the Euler line of triangle \(ABC\).

Let \(ABC\) be a triangle. Prove that the heights \(AD\), \(BE\), \(CF\) intersect in one point.

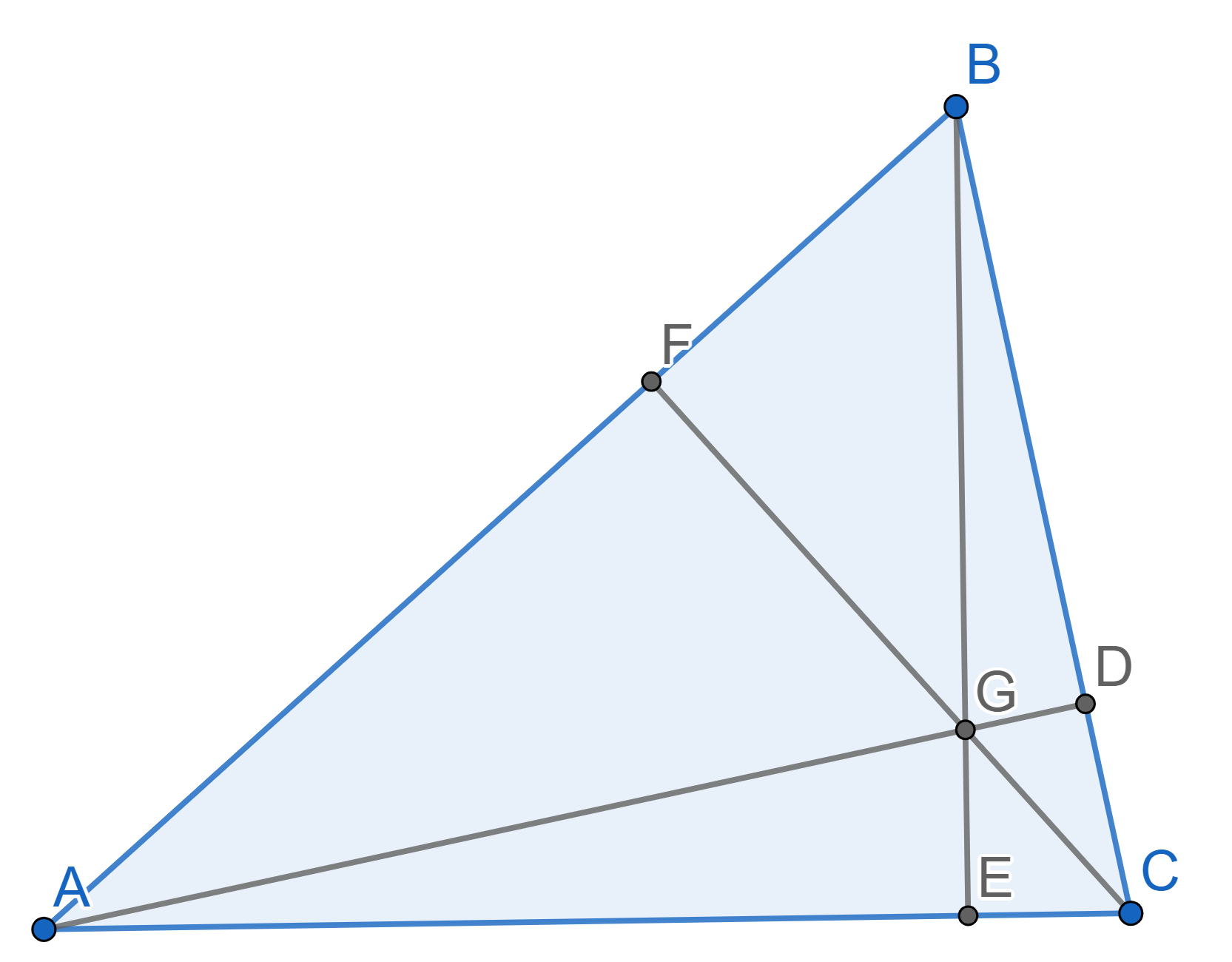
Let \(ABC\) be a triangle. Prove that the medians \(AD\), \(BE\), \(CF\) intersect in one point.

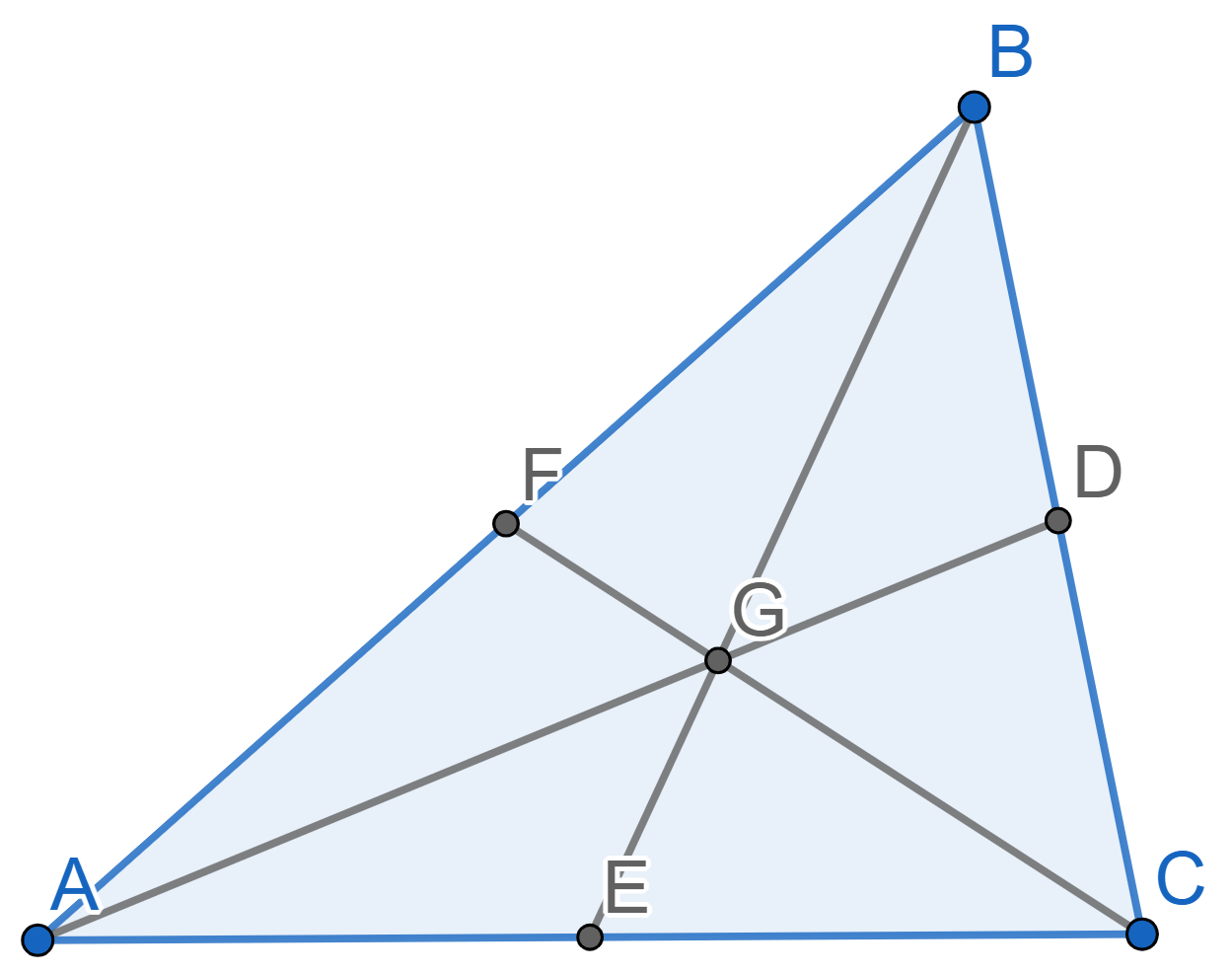
Let \(ABC\) be a triangle with medians \(AD\), \(BE\), \(CF\). Prove that the triangles \(ABC\) and \(DEF\) are similar. What is their similarity coefficient?

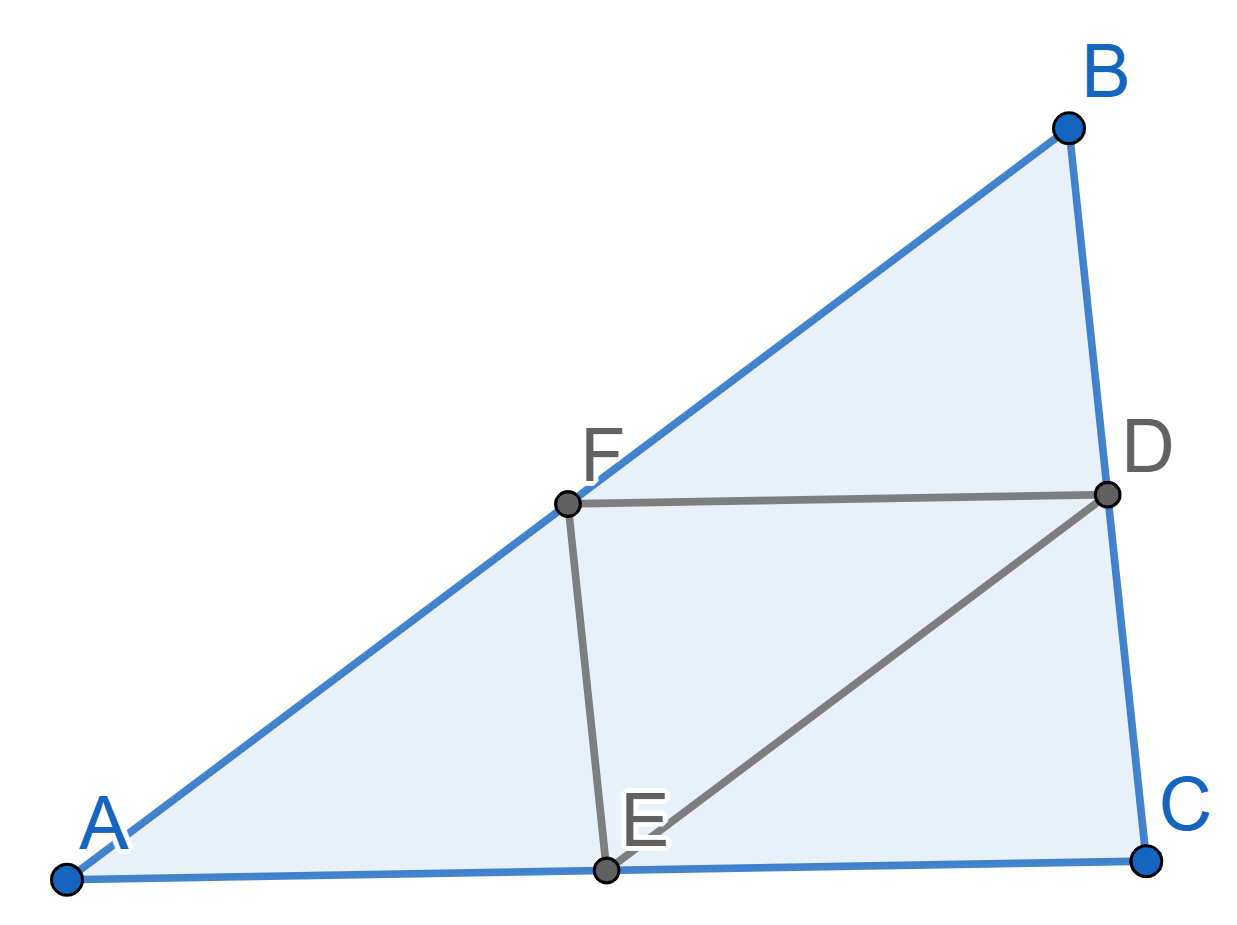
Let \(ABC\) be a triangle with midpoints \(D\) on the side \(BC\), \(E\) on the side \(AC\), and \(F\) on the side \(AB\). Prove that the perpendicular bisectors to the sides \(AB\), \(BC\), \(AC\) intersect at one point.

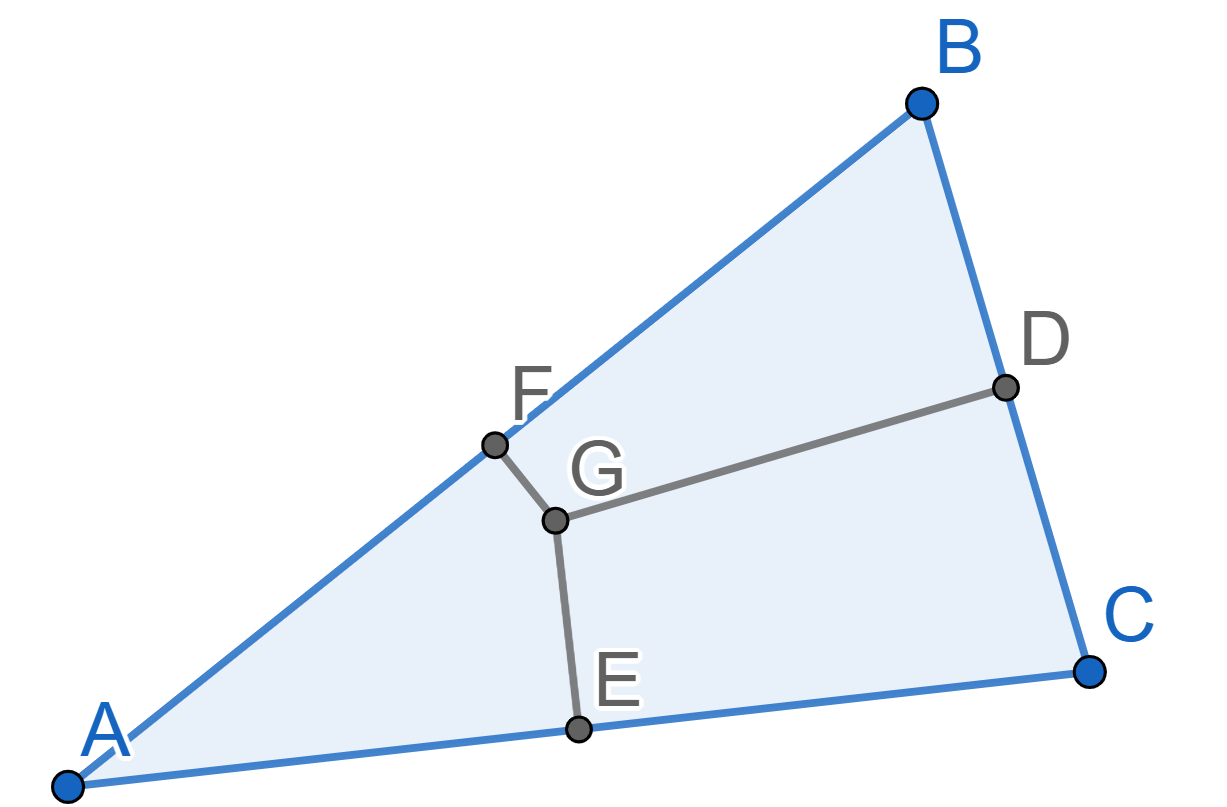
Let \(ABC\) be a triangle with midpoints \(D\) on the side \(BC\), \(E\) on the side \(AC\), and \(F\) on the side \(AB\). Let \(M\) be the point of intersection of all medians of the triangle \(ABC\), let \(H\) be the point of intersection of the heights \(AJ\), \(BI\) and \(CK\). Prove that the points \(D\), \(J\), \(I\), \(E\), \(F\) and \(K\) all lie on one circle.

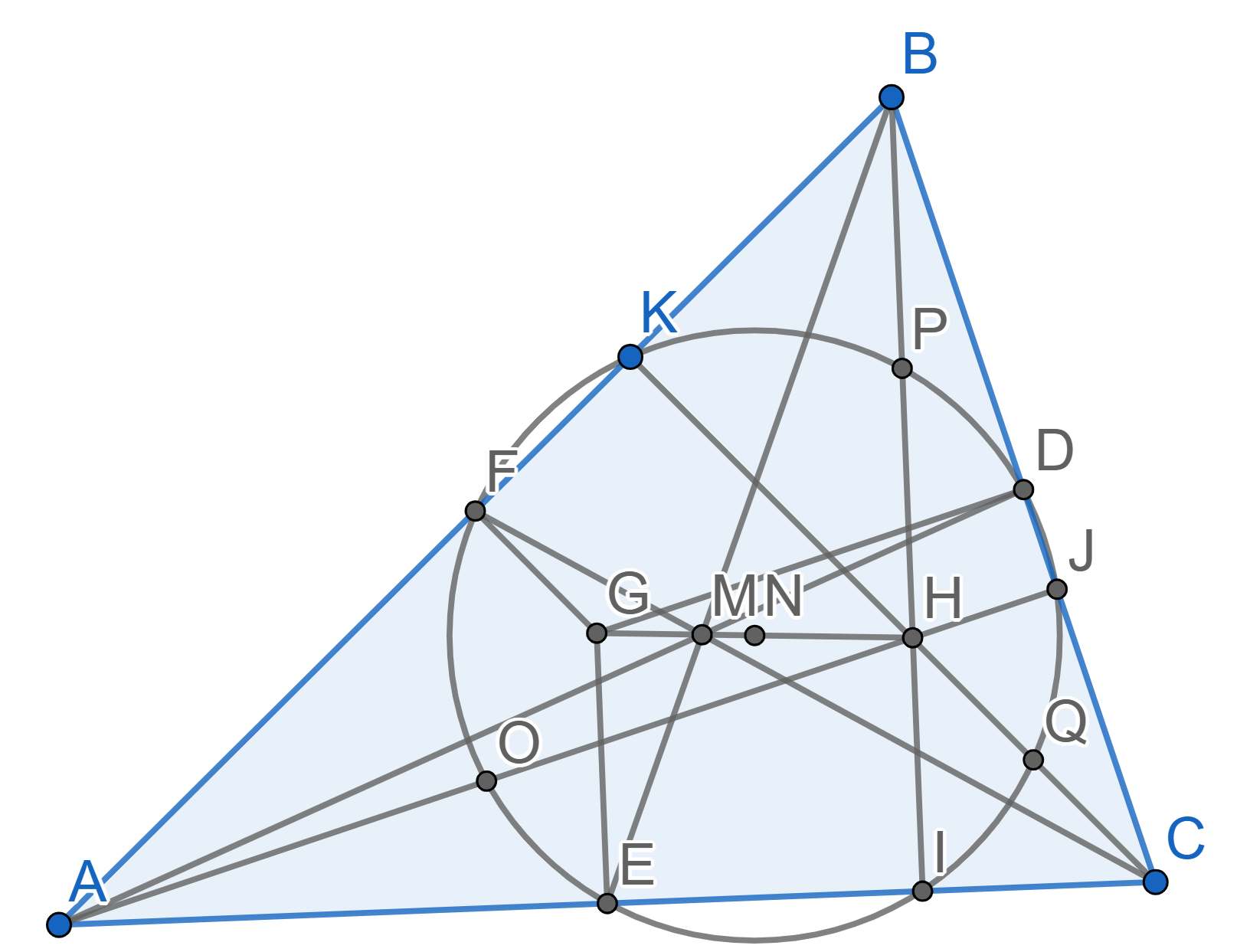
Let \(ABC\) be a triangle with midpoints \(D\) on the side \(BC\), \(E\) on the side \(AC\) and \(F\) on the side \(AB\). Let \(M\) be the point of intersection of all medians of the triangle \(ABC\) and let \(H\) be the point of intersection of the heights \(AJ\), \(BI\) and \(CK\). Consider the Euler circle of the triangle \(ABC\), which is the one that contains the points \(D,J,I,E,F,K\). This circle intersects the segments \(AH\), \(BH\) and \(CH\) at the points \(O\), \(P\) and \(Q\) respectively. Prove that \(O\), \(P\) and \(Q\) are the midpoints of the segments \(AH\), \(BH\) and \(CH\).