Problems

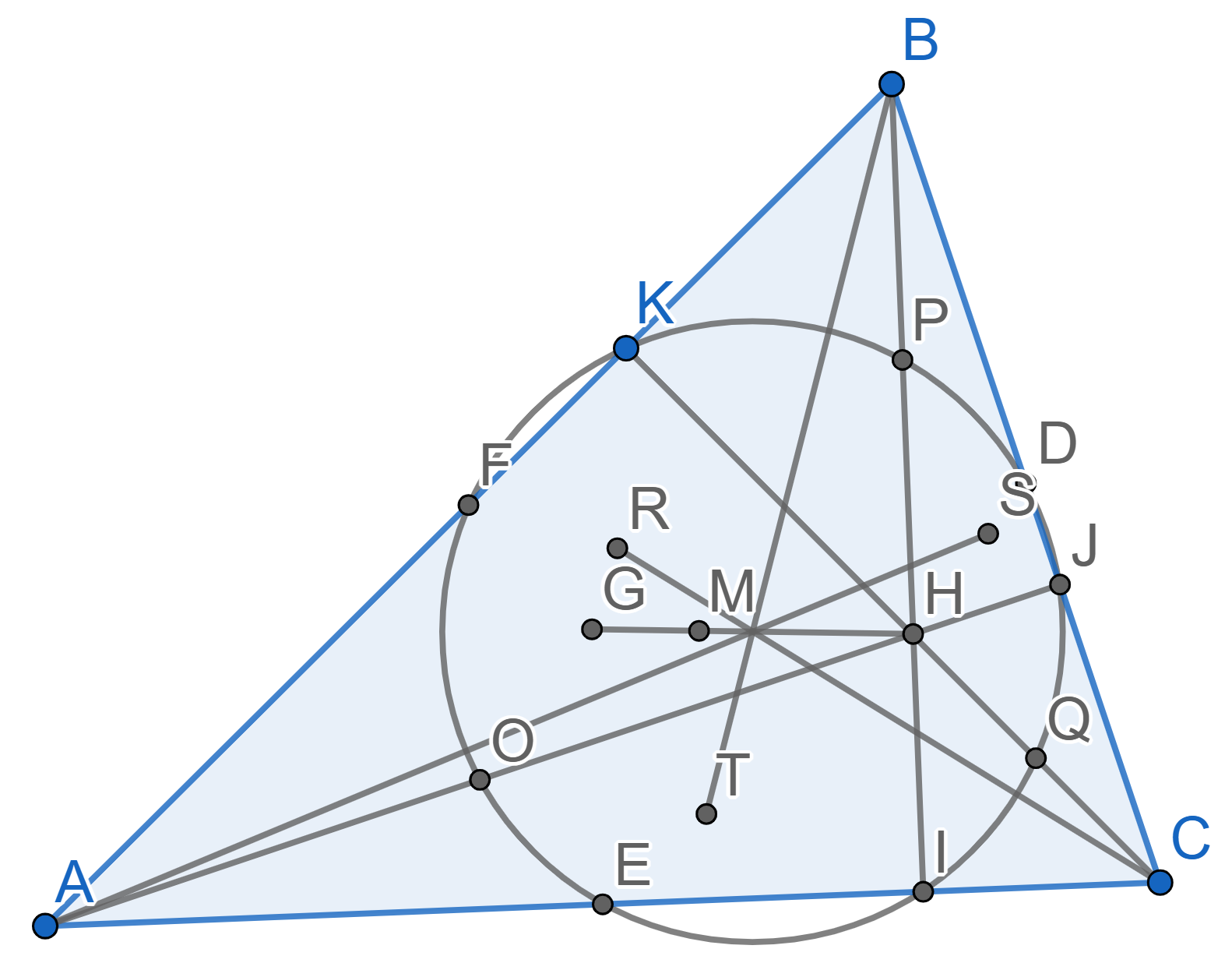
Consider the point \(H\) of intersection of the heights of the triangle \(ABC\). Prove that Euler lines of the triangles \(ABC\), \(ABH\), \(BCH\) and \(ACH\) intersect at one point. On the diagram below the points \(R,S,T\) are the points of intersection of medians in triangles \(ABH\), \(BCH\), and \(ACH\) respectively.

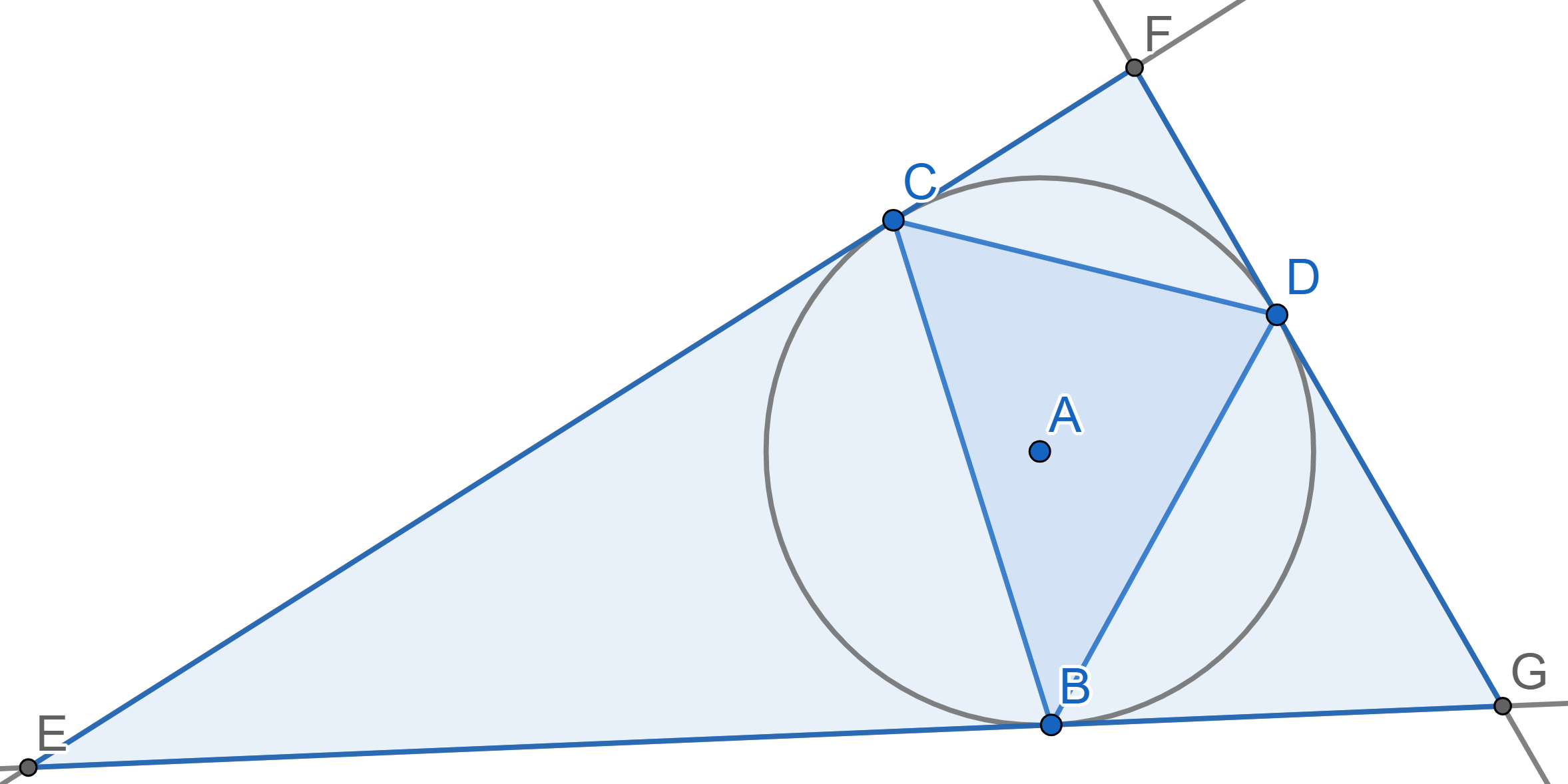
Consider the triangle \(BCD\), inscribed in a circle with center \(A\). The segments \(EF\), \(FG\) and \(EG\) are tangent to the circle at the points \(C\), \(D\) and \(B\) respectively. Prove that the Euler line of the triangle \(BCD\) passes through the center of the circle circumscribed around the triangle \(EFG\).

Take a regular dodecahedron as in the image. It has \(12\) regular pentagons as its faces, \(30\) edges, and \(20\) vertices. We can cut it with planes in various ways and the cut will be a polygon on a plane. Find out how many ways there are to cut a dodecahedron with a plane so that the polygon obtained is a regular hexagon.