Problems
a) The vertices (corners) in a regular polygon with 10 sides are colored black and white in an alternating fashion (i.e. one vertex is black, the next is white, etc). Two people play the following game. Each player in turn draws a line connecting two vertices of the same color. These lines must not have common vertices (i.e. must not begin or end on the same dot as another line) with the lines already drawn. The winner of the game is the player who made the final move. Which player, the first or the second, would win if the right strategy is used?
b) The same problem, but for a regular polygon with 12 sides.
The edges of a cube are assigned with integer values. For each vertex we look at the numbers corresponding to the three edges coming from this vertex and add them up. In case we get 8 equal results we call such cube “cute”. Are there any “cute” cubes with the following numbers corresponding to the edges:
(a) \(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12\);
(b) \(-6, -5, -4, -3, -2, -1, 1, 2, 3, 4, 5, 6\)?
The area of a rectangle is 1 cm\(^2\). Can its perimeter be greater than 1 km?
Let \(ABC\) be a triangle, prove that \(\angle ABC > 90^{\circ}\) if and only if the point \(B\) lies inside a circle with diameter \(AC\).
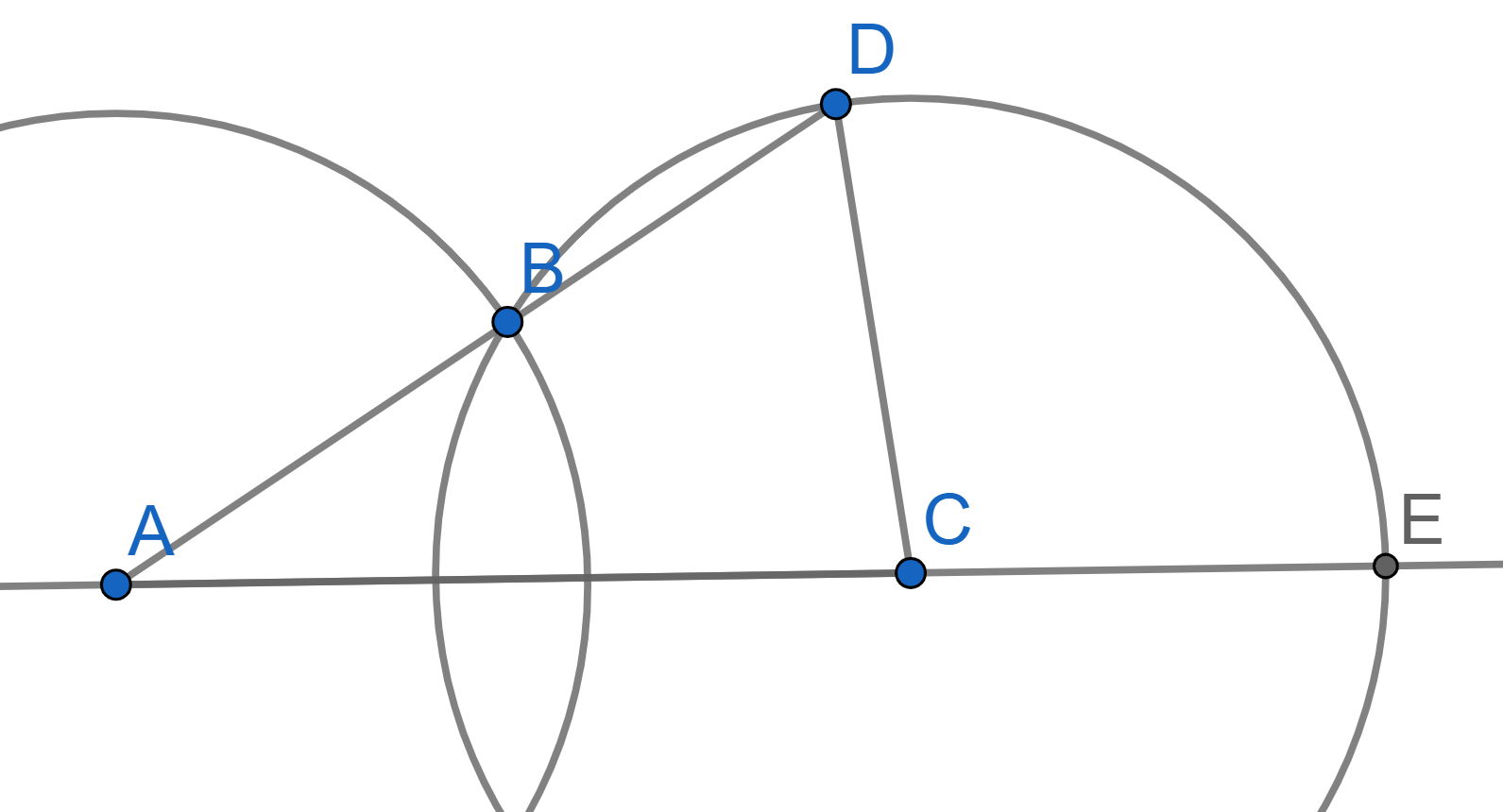
Two intersecting circles of radius \(R\) are given, and the distance between their centers is greater than \(R\). Prove that \(\angle ECD = 3\angle CAD\).
Two circles of radius \(R\) touch at point \(B\). On one of them, point \(D\) is chosen and on the other point \(E\) is chosen. These points have a property of \(\angle DBE = 90^{\circ}\). Prove that \(DE = 2R\).
Two circles of radius \(R\) intersect at points \(B\) and \(D\). Consider the perpendicular bisector of the segment \(BD\). This line meets the two circles again at points \(F\) and \(G\), both chosen on the same side of \(BD\). Prove that \[BD^2 + FG^2 = 4R^2.\]
Inside the rectangle \(ABCD\), the point \(E\) is taken. Prove that there exists a convex quadrilateral with perpendicular diagonals of lengths \(AB\) and \(BC\) whose sides are equal to \(AE\), \(BE\), \(CE\), \(DE\).
A parallelogram \(ABCD\) and a point \(E\) are given. Through the points \(A, B, C, D\), lines parallel to the straight lines \(EC, ED, EA,EB\), respectively, are drawn. Prove that they intersect at one point.
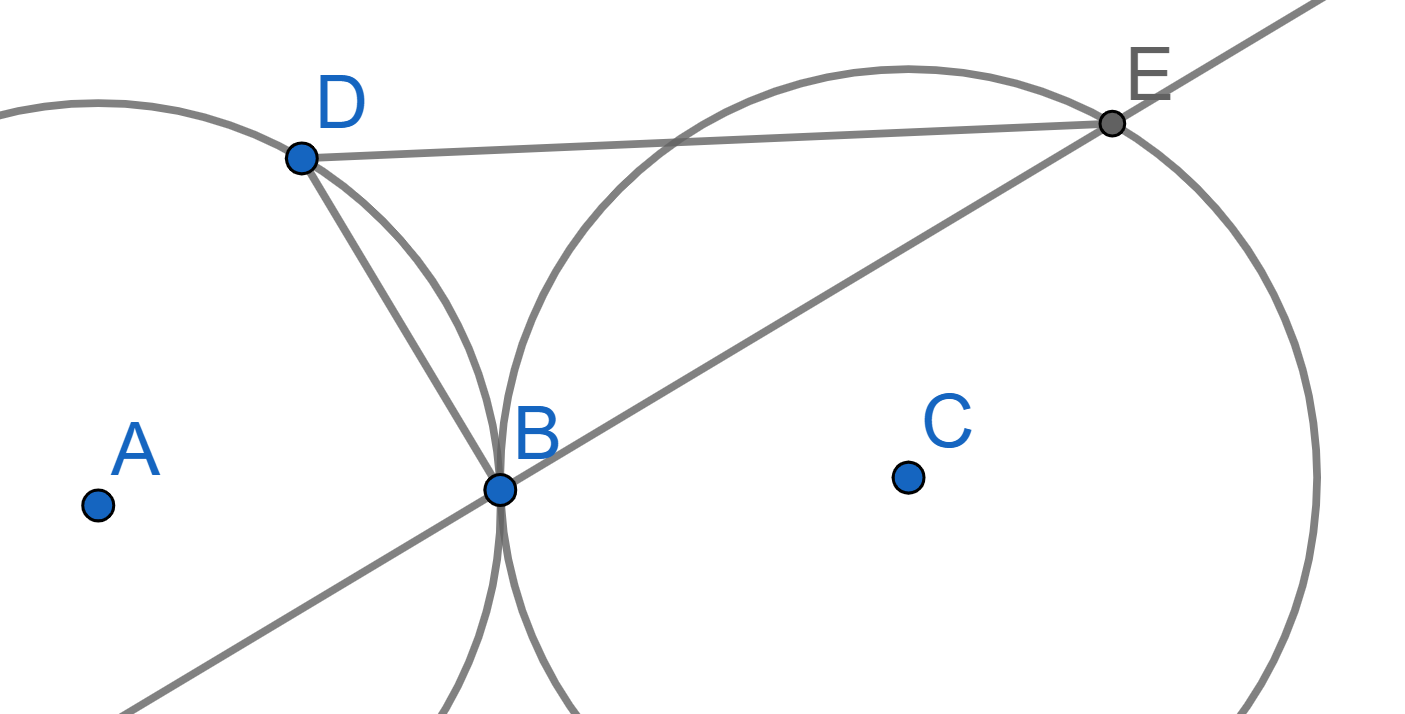
Two circles \(c\) and \(d\) are tangent at point \(B\). Two straight lines intersecting the first circle at points \(D\) and \(E\) and the second circle at points \(G\) and \(F\) are drawn through the point \(B\). Prove that \(ED\) is parallel to \(FG\).