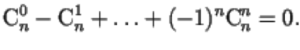Problems
In a burrow there is a family of 24 mice. Every night exactly four of them are sent to the warehouse for cheese.
Could it occur that at some point in time each mouse went to the warehouse with every other mouse exactly one time?
The grasshopper jumps on the interval \([0,1]\). On one jump, he can get from the point \(x\) either to the point \(x/3^{1/2}\), or to the point \(x/3^{1/2} + (1- (1/3^{1/2}))\). On the interval \([0,1]\) the point \(a\) is chosen.
Prove that starting from any point, the grasshopper can be, after a few jumps, at a distance less than \(1/100\) from point \(a\).
All of the sweets of different sorts in stock are arranged in \(n\) boxes, for which prices are set at \(1, 2, \dots , n\), respectively. It is required to buy such \(k\) of these boxes of the least total value, which contain at least \(k/n\) of the mass of all of the sweets. It is known that the mass of sweets in each box does not exceed the mass of sweets in any more expensive box.
a) What boxes should I buy when \(n = 10\) and \(k = 3\)?
b) The same question for arbitrary natural numbers \(n \geq k\).
Prove that for all \(x \in (0;\pi /2)\) for \(n > m\), where \(n, m\) are natural, we have the inequality \(2 | \sin^n x-\cos^n x | \leq 3 | \sin^m x-\cos^m x |\);
A New Year’s garland, hanging along the school corridor, consists of red and blue light bulbs. Next to each red light bulb there must necessarily be a blue one. What is the largest number of red light bulbs in this garland, if it consists of only 50 light bulbs?
Mark has 1000 identical cubes, each of which has one pair of opposite faces which are coloured white, another pair which are blue and a third pair that are red. He made a large \(10 \times 10 \times 10\) cube from them, joining cubes to one another which have the same coloured faces. Prove that the large cube has a face which is solidly one colour.
In a country coming out of each city there are 100 roads and from each city it is possible to reach any other. One road was closed for repairs. Prove that even now you can get from every city to any other.
Prove that out of \(n\) objects an even number of objects can be chosen in \(2^{n-1}\) ways.
Prove that every number \(a\) in Pascal’s triangle is equal to
a) the sum of the numbers of the previous right diagonal, starting from the leftmost number up until the one to the right above the number \(a\).
b) the sum of the numbers of the previous left diagonal, starting from the leftmost number to the one to left of the number which is above \(a\).