We solve problems

Problem #PRU-98408

Problems Geometry Plane geometry Circles Central angle. Arc length and circumference Diameter, chords, and secants Chords and secants (other) Methods Pigeonhole principle Pigeonhole principle (finite number of poits, lines etc.) Polygons Regular polygons

12–14 4.0

In a regular polygon with \(25\) vertices, all the diagonals are drawn.

Prove that there are no nine diagonals passing through one interior point of the shape.

Problem #PRU-98426

Problems Geometry Plane geometry Quadrilateral Parallelogram Special cases Rectangles and squares. Criteria and properties

11–13 3.0

A square is cut by 18 straight lines, 9 of which are parallel to one side of the square and the other 9 parallel to the other – perpendicular to the first 9 – dividing the square into 100 rectangles. It turns out that exactly 9 of these rectangles are squares. Prove that among these 9 squares there will be two that are identical.

Problem #PRU-98652

Problems Geometry Plane geometry Area Area ratio Area ratio of similar figures

11–12 1.0

The population of China is one billion people. It would seem that on a map of China with a scale of 1 : 1,000,000 (1 cm : 10 km), it would be possible to fit a million times fewer people than there is in the whole country. However, in fact, not only 1000, but even 100 people will not be able to be placed on this map. Can you explain this contradiction?

Problem #PRU-102815

Problems Geometry Solid geometry Visual geometry in space

11–13 2.0

Propose a method for measuring the diagonal of a conventional brick, which is easily realied in practice (without the Pythagorean theorem).

Problem #PRU-103008

Problems Algebra and arithmetic Arithmetics. Mental maths Geometry Solid geometry Volume Ratio of volumes

10–11 2.0

When Gulliver came to Lilliput, he found that there all things were exactly 12 times shorter than in his homeland. Can you say how many Lilliputian matchboxes fit into one of Gulliver’s matchboxes?

Problem #PRU-103818

Problems Geometry Plane geometry Quadrilateral Parallelogram Special cases Rectangles and squares. Criteria and properties

11–12 2.0

Which rectangles with whole sides are there more of: with perimeter of 1996 or with perimeter of 1998? (The rectangles \(a \times b\) and \(b \times a\) are assumed to be the same).

Problem #PRU-103824

Problems Geometry Solid geometry Spheres Circle on a sphere Visual geometry in space

11–13 2.0

A globe has 17 parallels and 24 meridians. How many parts is the globe’s surface divided into? The meridian is an arc connecting the North Pole with the South Pole. A parallel is a circle parallel to the equator (the equator is also a parallel).

Problem #PRU-103888

Problems Methods Algebraic methods Proof by exhaustion Geometry Solid geometry Visual geometry in space

11–12 2.0

A square napkin was folded in half, the resulting rectangle was then folded in half again (see the figure). The resulting square was then cut with scissors (in a straight line). Could the napkin have been broken up a) into 2 parts? b) into 3 parts? c) into 4 parts? d) into 5 parts? If yes – illustrate such a cut, if not – write the word “no”.

Problem #PRU-103947

Problems Geometry Plane geometry Area

10–12 2.0

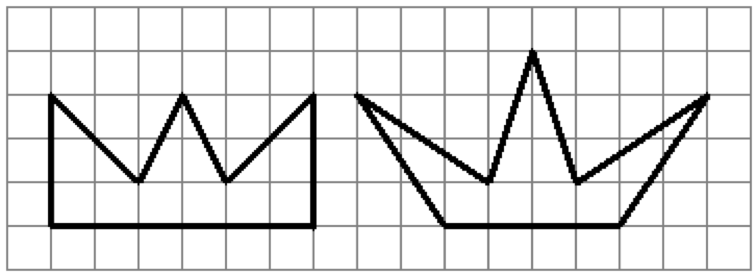
Find the area of the figures shown below.

Problem #PRU-104021

Problems Geometry Solid geometry Parallelepipeds Special cases of parallelepipeds Cube Number Theory Divisibility Odd and even numbers Methods Pigeonhole principle Pigeonhole principle (other)

12–13 2.0

a) A 1 or a 0 is placed on each vertex of a cube. The sum of the 4 adjacent vertices is written on each face of the cube. Is it possible for each of the numbers written on the faces to be different?

b) The same question, but if 1 and \(-1\) are used instead.