We solve problems

Problem #PRU-97956

Problems Geometry Plane geometry Polygons Regular polygons Discrete Mathematics Algorithm Theory Game theory Symmetric strategies

12–14 2.0

a) The vertices (corners) in a regular polygon with 10 sides are colored black and white in an alternating fashion (i.e. one vertex is black, the next is white, etc). Two people play the following game. Each player in turn draws a line connecting two vertices of the same color. These lines must not have common vertices (i.e. must not begin or end on the same dot as another line) with the lines already drawn. The winner of the game is the player who made the final move. Which player, the first or the second, would win if the right strategy is used?

b) The same problem, but for a regular polygon with 12 sides.

Problem #PRU-100430

Problems Geometry Solid geometry Parallelepipeds Special cases of parallelepipeds Cube Discrete Mathematics Set theory and logic Logic and set theory

The edges of a cube are assigned with integer values. For each vertex we look at the numbers corresponding to the three edges coming from this vertex and add them up. In case we get 8 equal results we call such cube “cute”. Are there any “cute” cubes with the following numbers corresponding to the edges:

(a) \(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12\);

(b) \(-6, -5, -4, -3, -2, -1, 1, 2, 3, 4, 5, 6\)?

Problem #PRU-100454

Problems Discrete Mathematics Set theory and logic Mathematical logic Paradoxes Geometry Plane geometry Quadrilateral Parallelogram Special cases Rectangles and squares. Criteria and properties

The area of a rectangle is 1 cm\(^2\). Can its perimeter be greater than 1 km?

Problem #PRU-57301

Problems Geometry Plane geometry Geometrical inequalities Geometric inequalities (other)

13–14 3.0

Let \(ABC\) be a triangle, prove that \(\angle ABC > 90^{\circ}\) if and only if the point \(B\) lies inside a circle with diameter \(AC\).

Problem #PRU-57633

Problems Geometry Plane geometry Triangles Relationship of side lengths and angles of a triangle. Solving triangles. Relations between sides and angles of a triangle (other)

13–15 2.0

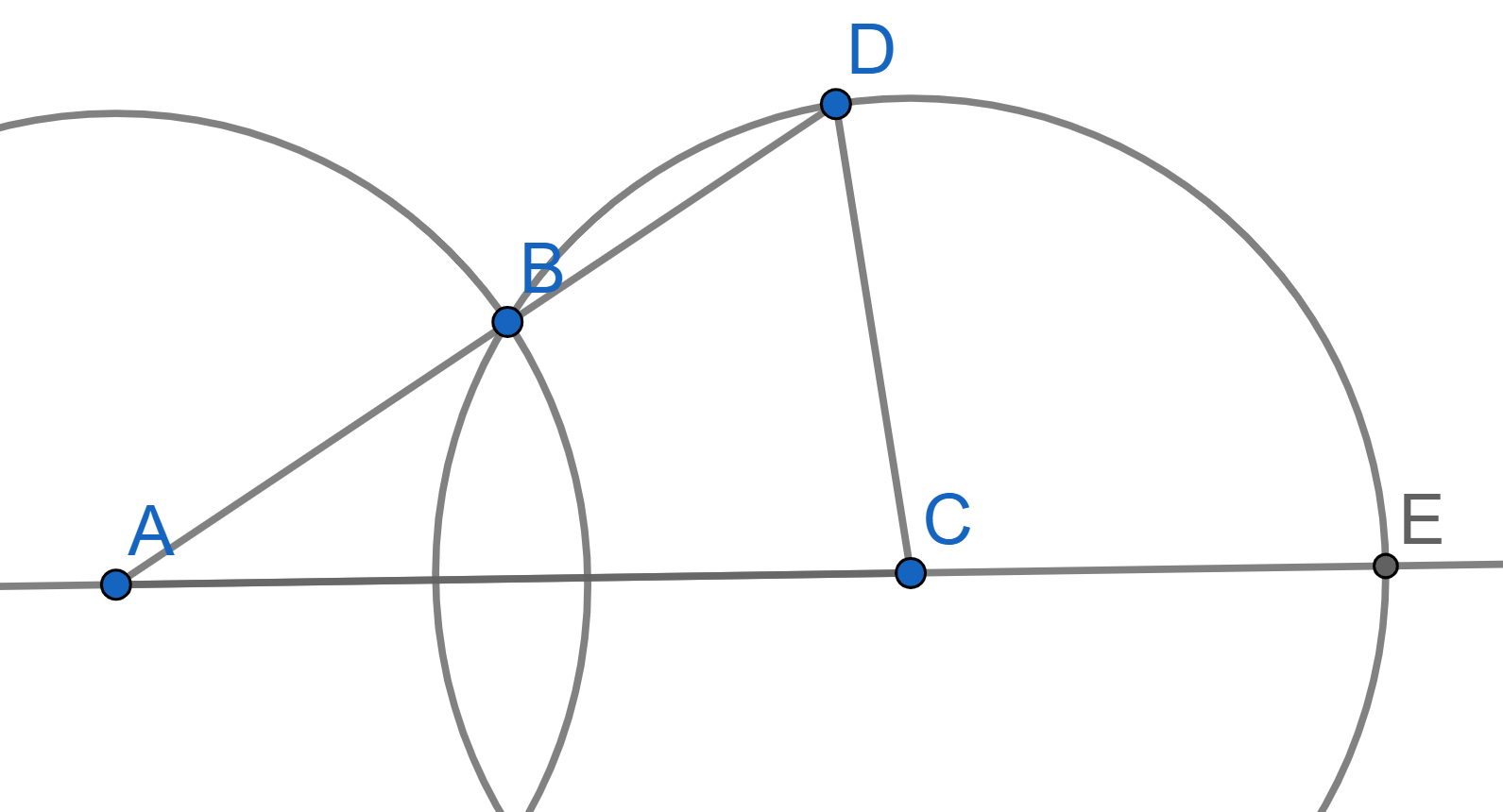
Two intersecting circles of radius \(R\) are given, and the distance between their centers is greater than \(R\). Prove that \(\angle ECD = 3\angle CAD\).

Problem #PRU-57808

Problems Geometry Plane geometry Plane transformations Parallel translation

13–15 4.0

Two circles of radius \(R\) touch at point \(B\). On one of them, point \(D\) is chosen and on the other point \(E\) is chosen. These points have a property of \(\angle DBE = 90^{\circ}\). Prove that \(DE = 2R\).

Problem #PRU-57809

Problems Geometry Plane geometry Plane transformations Parallel translation

13–15 3.0

Two circles of radius \(R\) intersect at points \(B\) and \(D\). Consider the perpendicular bisector of the segment \(BD\). This line meets the two circles again at points \(F\) and \(G\), both chosen on the same side of \(BD\). Prove that \[BD^2 + FG^2 = 4R^2.\]

Problem #PRU-57810

Problems Geometry Plane geometry Plane transformations Parallel translation

13–14 2.0

Inside the rectangle \(ABCD\), the point \(E\) is taken. Prove that there exists a convex quadrilateral with perpendicular diagonals of lengths \(AB\) and \(BC\) whose sides are equal to \(AE\), \(BE\), \(CE\), \(DE\).

Problem #PRU-57836

Problems Geometry Solid geometry Space transformations Isometry Point symmetry

13–15 3.0

A parallelogram \(ABCD\) and a point \(E\) are given. Through the points \(A, B, C, D\), lines parallel to the straight lines \(EC, ED, EA,EB\), respectively, are drawn. Prove that they intersect at one point.

Problem #PRU-57976

Problems Geometry Plane geometry Plane transformations Similarity Homothetic transformations, rotations of homothetic transformations

14–16 3.0

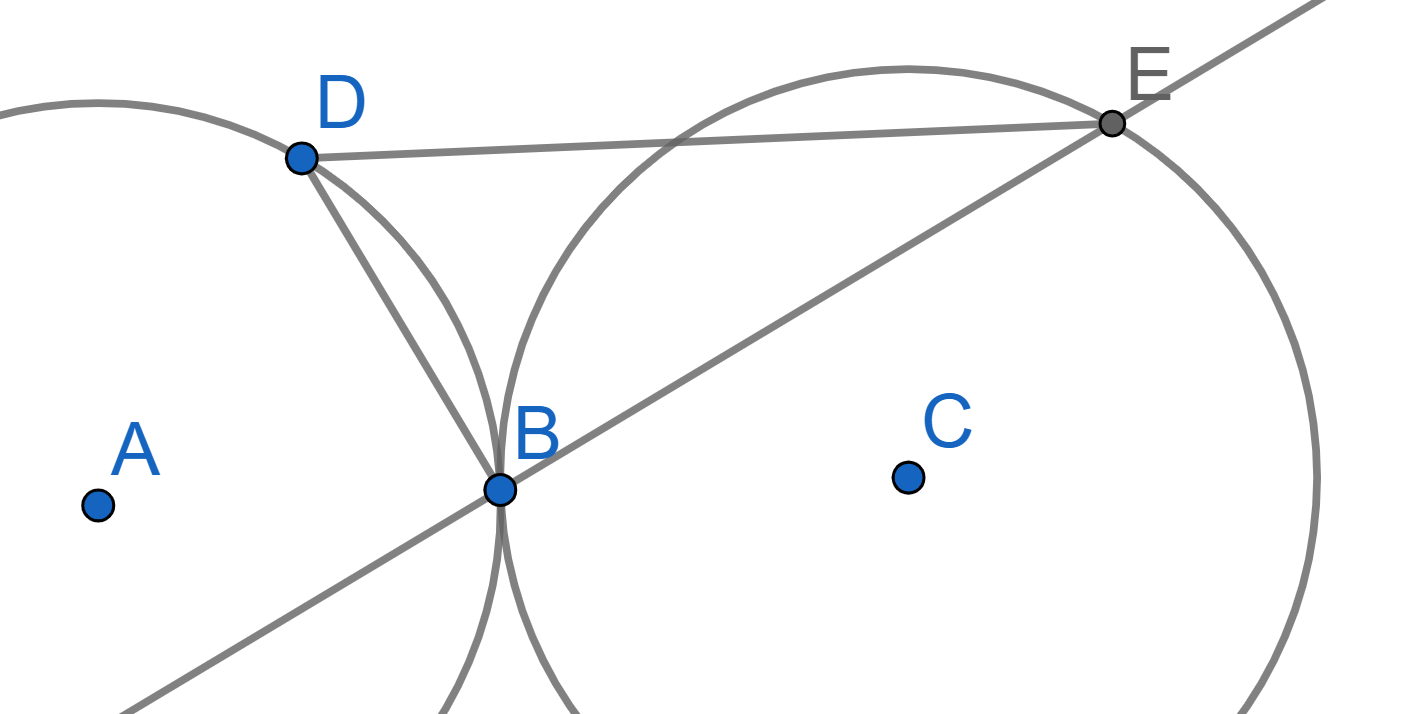
Two circles \(c\) and \(d\) are tangent at point \(B\). Two straight lines intersecting the first circle at points \(D\) and \(E\) and the second circle at points \(G\) and \(F\) are drawn through the point \(B\). Prove that \(ED\) is parallel to \(FG\).