Problems

Age
Difficulty
 Clear filters
Found: 501
Problem #PRU-5016
 10–13  2.0

  • We call two figures congruent if their corresponding sides and angles are equal. Let \(ABD\) an \(A'B'D'\) be two right-angled triangles with right angle \(D\). Then if \(AD=A'D'\) and \(AB=A'B'\) then the triangles \(ABD\) and \(A'B'D'\) are congruent.

  • It follows from the previous statement that if two lines \(AB\) and \(CD\) are parallel than angles \(BCD\) and \(CBA\) are equal.

Problem #PRU-5017
 10–13  2.0

We prove the other two assertions from the description:

  • The sum of all internal angles of a triangle is also \(180^{\circ}\).

  • In an isosceles triangle (which has two sides of equal lengths), two angles touching the third side are equal.

Problem #PRU-5018
 10–13  2.0

In the triangle \(ABC\) the sides are compared as following: \(AC>BC>AB\). Prove that the angles are compared as follows: \(\angle B > \angle A > \angle C\).

Problem #PRU-53644
 12–14  4.0

Consider a quadrilateral \(ABCD\). Choose a point \(E\) on side \(AB\). A line parallel to the diagonal \(AC\) is drawn through \(E\) and meets \(BC\) at \(F\). Then a line parallel to the other diagonal \(BD\) is drawn through \(F\) and meets \(CD\) at \(G\). And then a line parallel to the first diagonal \(AC\) is drawn through \(G\) and meets \(DA\) at \(H\). Prove the \(EH\) is parallel to the diagonal \(BD\).

Problem #PRU-58221
 12–14  3.0

Cut an arbitrary triangle into parts that can be used to build a triangle that is symmetrical to the original triangle with respect to some straight line (the pieces cannot be inverted, they can only be rotated on the plane).

Problem #PRU-10002
 10–14

Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a square, or slightly harder in a shape of a given rectangle.

Problem #PRU-10006
 10–14  3.0

Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a hexagon

Problem #PRU-10005
 10–14

Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a given triangle.

Problem #PRU-10004
 10–14

Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a shape like this

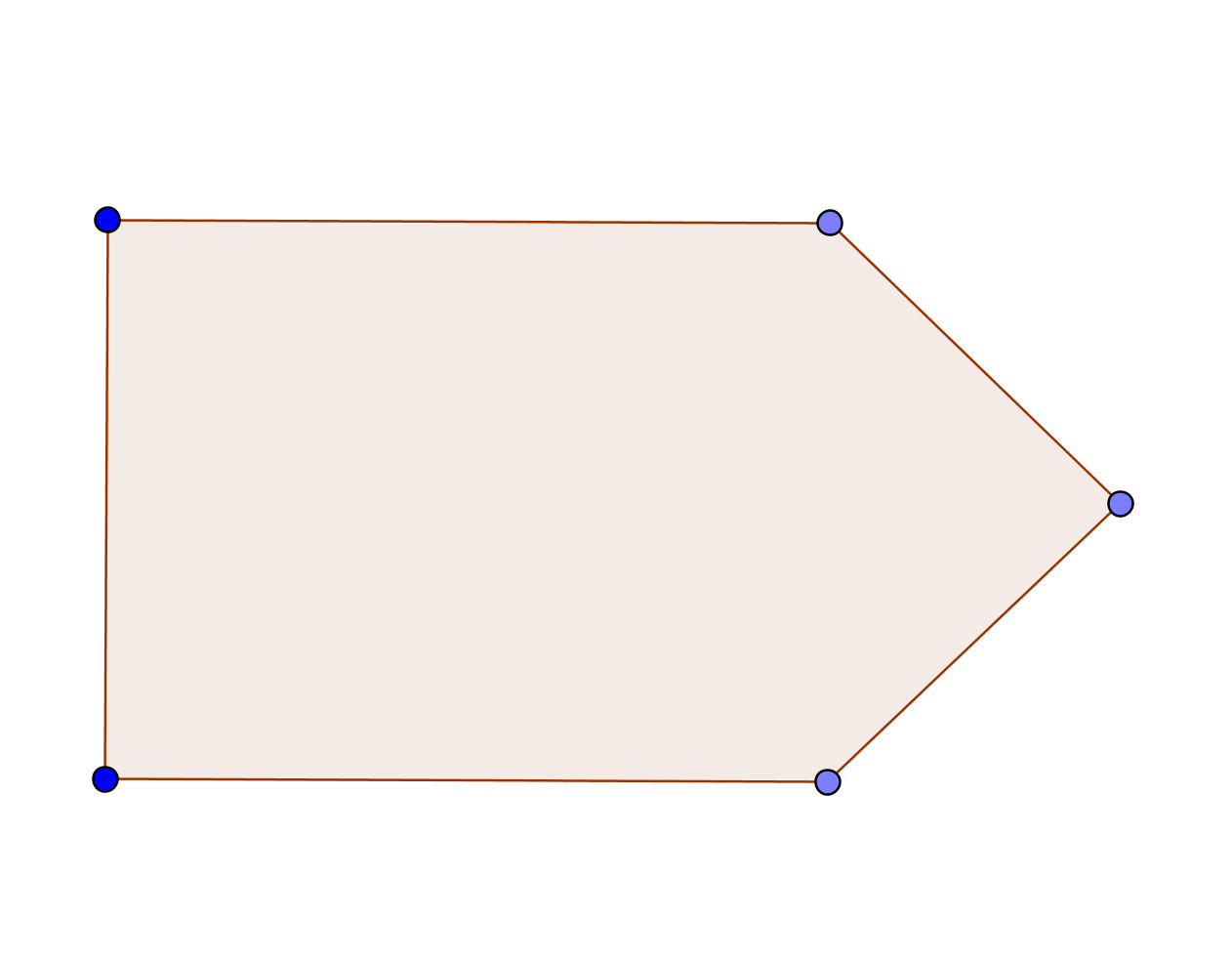
image

Problem #PRU-10003
 10–14  3.0

Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a parallelogram.