Problems

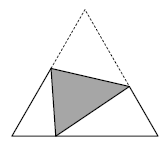
A equilateral triangle made of paper bends in a straight line so that one of the vertices falls on the opposite side as shown on the picture. Prove that the corresponding angles of the two white triangles are equal.

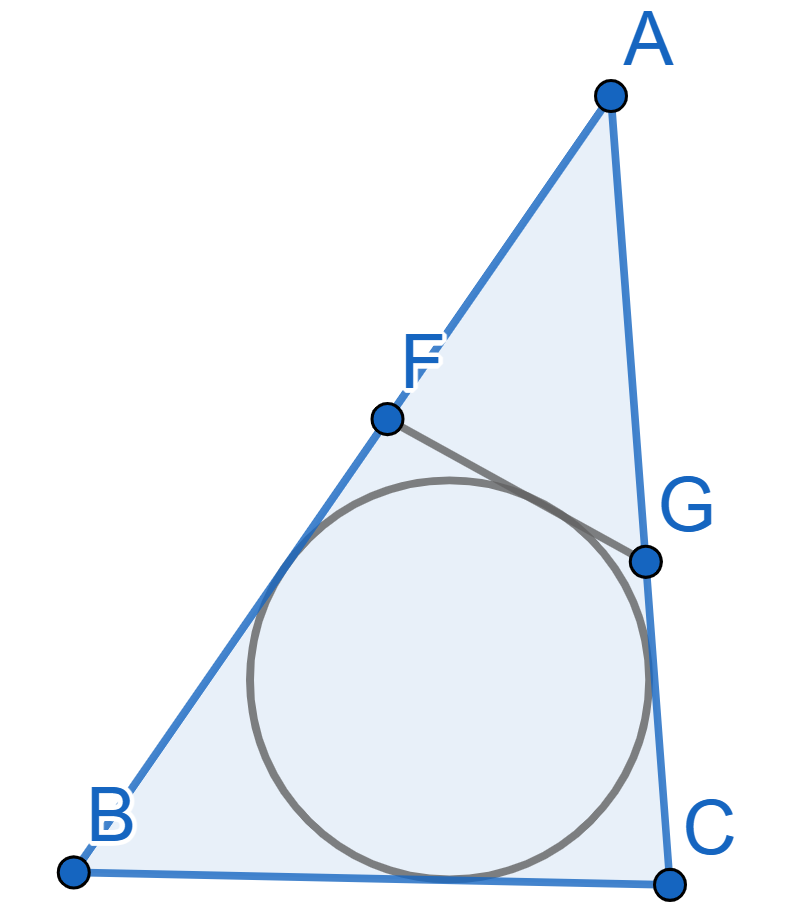
A circle is inscribed into the triangle \(ABC\) with sides \(BC=6, AC=10\) and \(AB= 12\). A line tangent to the circle intersects two longer sides of the triangle \(AB\) and \(AC\) at the points \(F\) and \(G\) respectively. Find the perimeter of the triangle \(AFG\).

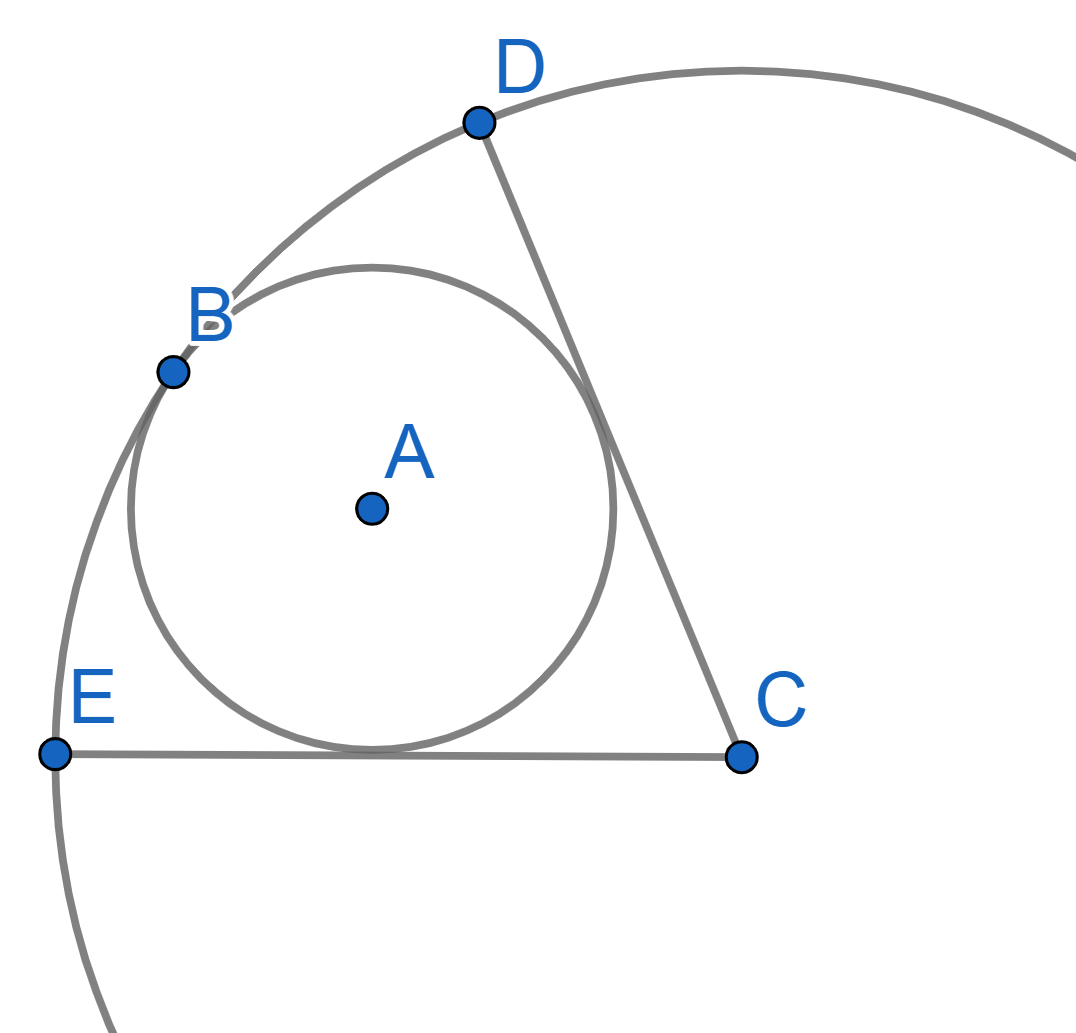
Two circles are tangent to each other and the smaller circle with the center \(A\) is located inside the larger circle with the center \(C\). The radii \(CD\) and \(CE\) are tangent to the smaller circle and the angle \(\angle DCE = 60^{\circ}\). Find the ratio of the radii of the circles.

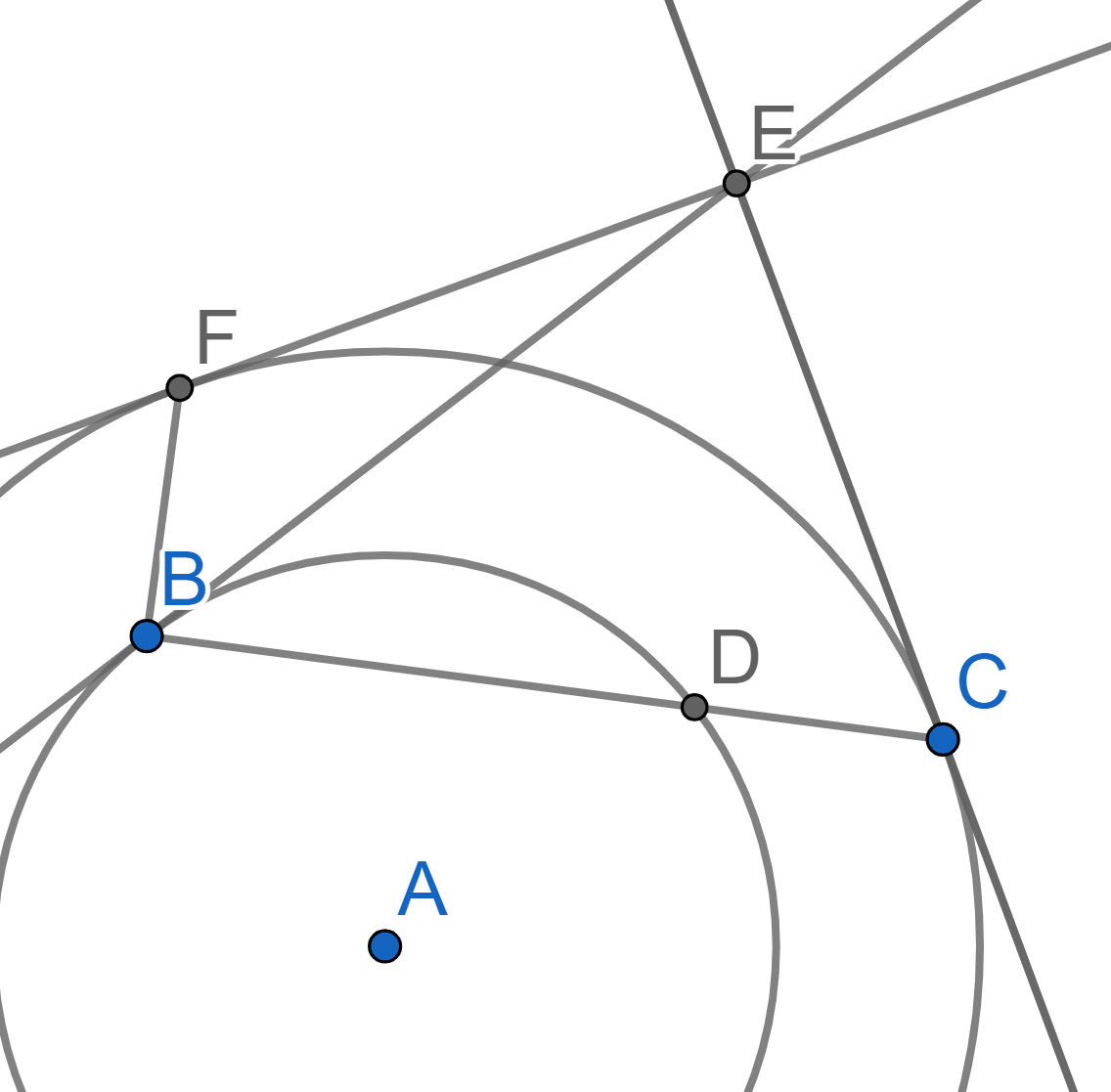
Let \(C_1\) and \(C_2\) be two concentric circles with \(C_1\) inside \(C_2\) and the center \(A\). Let \(B\) and \(D\) be two points on \(C_1\) that are not diametrically opposite. Extend the segment \(BD\) past \(D\) until it meets the circle \(C_2\) in \(C\). The tangent to \(C_2\) at \(C\) and the tangent to \(C_1\) at \(B\) meet in a point \(E\). Draw from \(E\) the second tangent to \(C_2\) which meets \(C_2\) at the point \(F\). Show that \(BE\) bisects angle \(\angle FBC\).

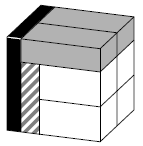
Michael made a cube with edge \(1\) out of eight bars as in the picture. All \(8\) bars have the same volume. The dimensions of the grey bars are the same as each other. Similarly, the dimensions of the white bars are the same as each other. Find the lengths of the edges of the white bars.

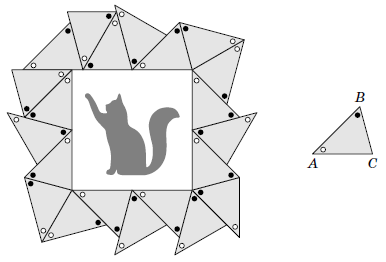
Peter went to the Museum of Modern Art and saw a square painting in a frame of an unusual shape. The frame consisted of \(21\) congruent triangles. Peter was interested in what the angles of these triangles were equal to. Help him find these angles.

Let \(a\), \(b\) and \(c\) be the three side lengths of a triangle. Does there exist a triangle with side lengths \(a+1\), \(b+1\) and \(c+1\)? Does it depend on what \(a\), \(b\) and \(c\) are?

There is a triangle with side lengths \(a\), \(b\) and \(c\). Can you form a triangle with side lengths \(\frac{a}{b}\), \(\frac{b}{c}\) and \(\frac{c}{a}\)? Does it depend on what \(a\), \(b\) and \(c\) are? Give a proof if it is always possible or never possible. Otherwise, construct examples to show the dependence on \(a\), \(b\) and \(c\).
Recall that a triangle can be drawn with side lengths \(x\), \(y\) and \(z\) if and only if \(x+y>z\), \(y+z>x\) and \(z+x>y\).

There is a triangle with side lengths \(a\), \(b\) and \(c\). Does there exist a triangle with side lengths \(|a-b|\), \(|b-c|\) and \(|c-a|\)? Does it depend on what \(a\), \(b\) and \(c\) are?
Recall that a triangle can be formed with side lengths \(x\), \(y\) and \(z\) if and only if all the inequalities \(x+y>z\), \(y+z>x\) and \(z+x>y\) hold.

There is a triangle with side lenghts \(a\), \(b\) and \(c\). Does there exist a triangle with sides of lengths \(a^2+bc\), \(b^2+ca\) and \(c^2+ab\)? Does it depend on the values of \(a\), \(b\) and \(c\)?