Problems
Let \(ABCD\) be a square and let \(X\) be any point on side \(BC\) between \(B\) and \(C\). Let \(Y\) be the point on line \(CD\) such that \(BX=YD\) and \(D\) is between \(C\) and \(Y\). Prove that the midpoint of \(XY\) lies on diagonal \(BD\).
Let \(ABCD\) be a trapezium such that \(AB\) is parallel to \(CD\). Let \(E\) be the intersection of diagonals \(AC\) and \(BD\). Suppose that \(AB=BE\) and \(AC=DE\). Prove that the internal angle bisector of \(\angle BAC\) is perpendicular to \(AD\).
Let \(ABC\) be an isosceles triangle with \(AB=AC\). Point \(D\) lies on side \(AC\) such that \(BD\) is the angle bisector of \(\angle ABC\). Point \(E\) lies on side \(BC\) between \(B\) and \(C\) such that \(BE=CD\). Prove that \(DE\) is parallel to \(AB\).
\(ABCD\) is a rectangle with side lengths \(AB=CD=1\) and \(BC=DA=2\). Let \(M\) be the midpoint of \(AD\). Point \(P\) lies on the opposite side of line \(MB\) to \(A\), such that triangle \(MBP\) is equilateral. Find the value of \(\angle PCB\).
A rectangular sheet of paper is folded so that one corner lies on top of the corner diagonally opposite. The resulting shape is a pentagon whose area is \(20\%\) one-sheet-thick, and \(80\%\) two-sheets-thick. Determine the ratio of the two sides of the original sheet of paper.
Suppose you only knew the area formula of a triangle for right-angled triangles. That is, if a base with length \(b\) and a height \(h\) of a triangle meet at a right angle, you know that the area of the triangle is \(\frac{1}{2}bh\). Can you prove the usual area formula for a general triangle?
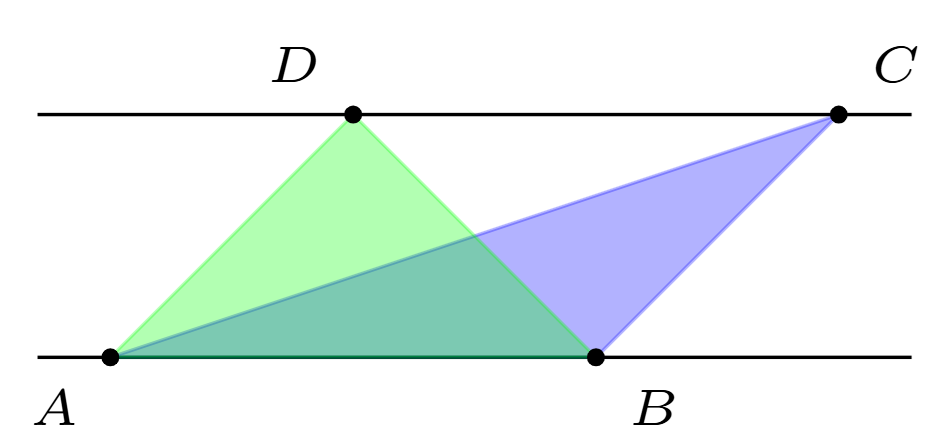
There is a pair of parallel lines. The point \(A\) and \(B\) lie on one of the lines. The point \(C\) and \(D\) lies on the other line. We can form triangles \(\triangle ABC\) and \(\triangle ABD\). Prove that the areas of triangles \(\triangle ABC\) and \(\triangle ABD\) are equal.
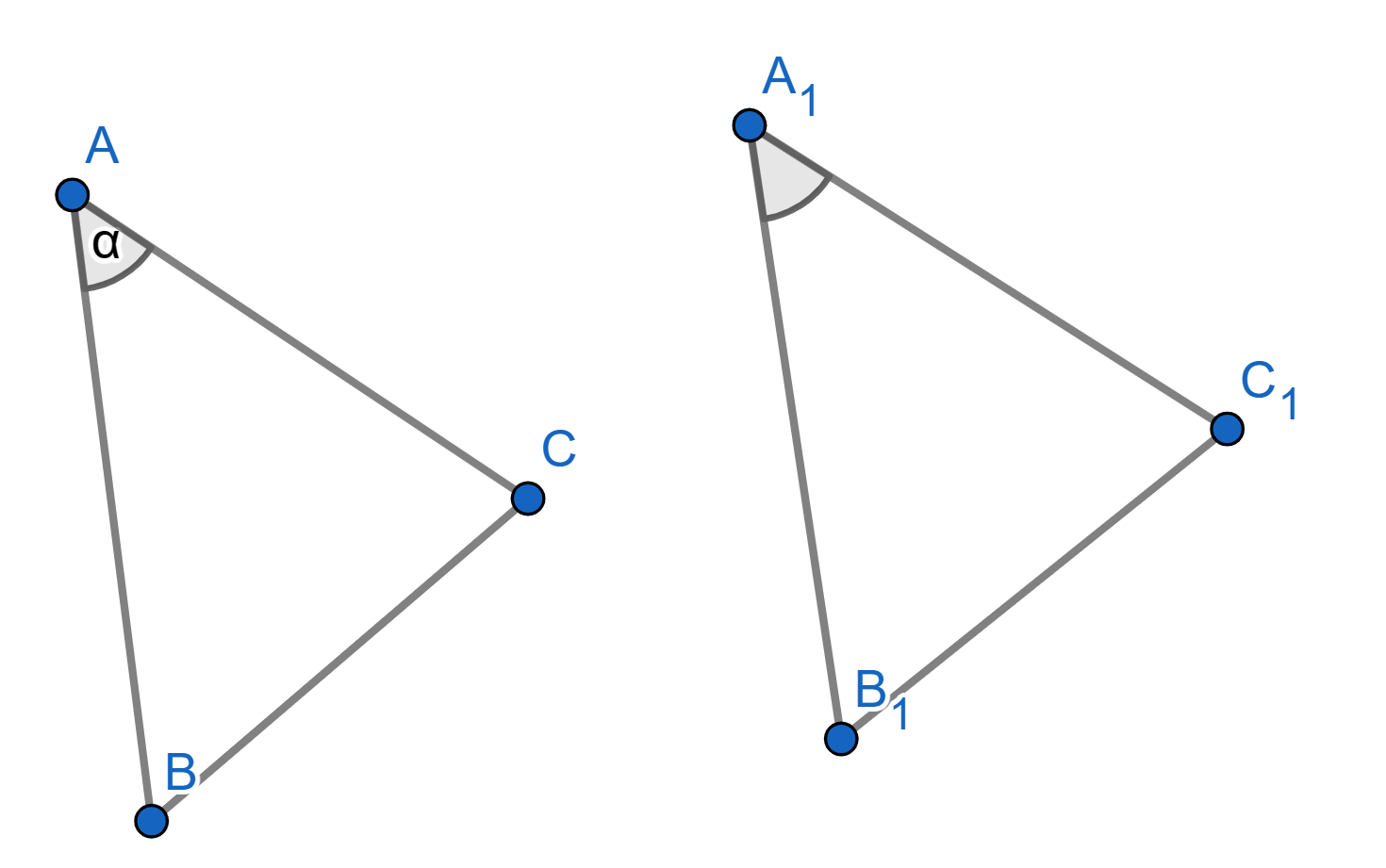
Let \(ABC\) and \(A_1B_1C_1\) be two triangles with the following properties: \(AB = A_1B_1\), \(AC = A_1C_1\), and angles \(\angle BAC = \angle B_1A_1C_1\). Then the triangles \(ABC\) and \(A_1B_1C_1\) are congruent. This is usually known as the “side-angle-side" criterion for congruence.
In the triangle \(\triangle ABC\) the sides \(AC\) and \(BC\) are equal. Prove that the angles \(\angle CAB\) and \(\angle CBA\) are equal.
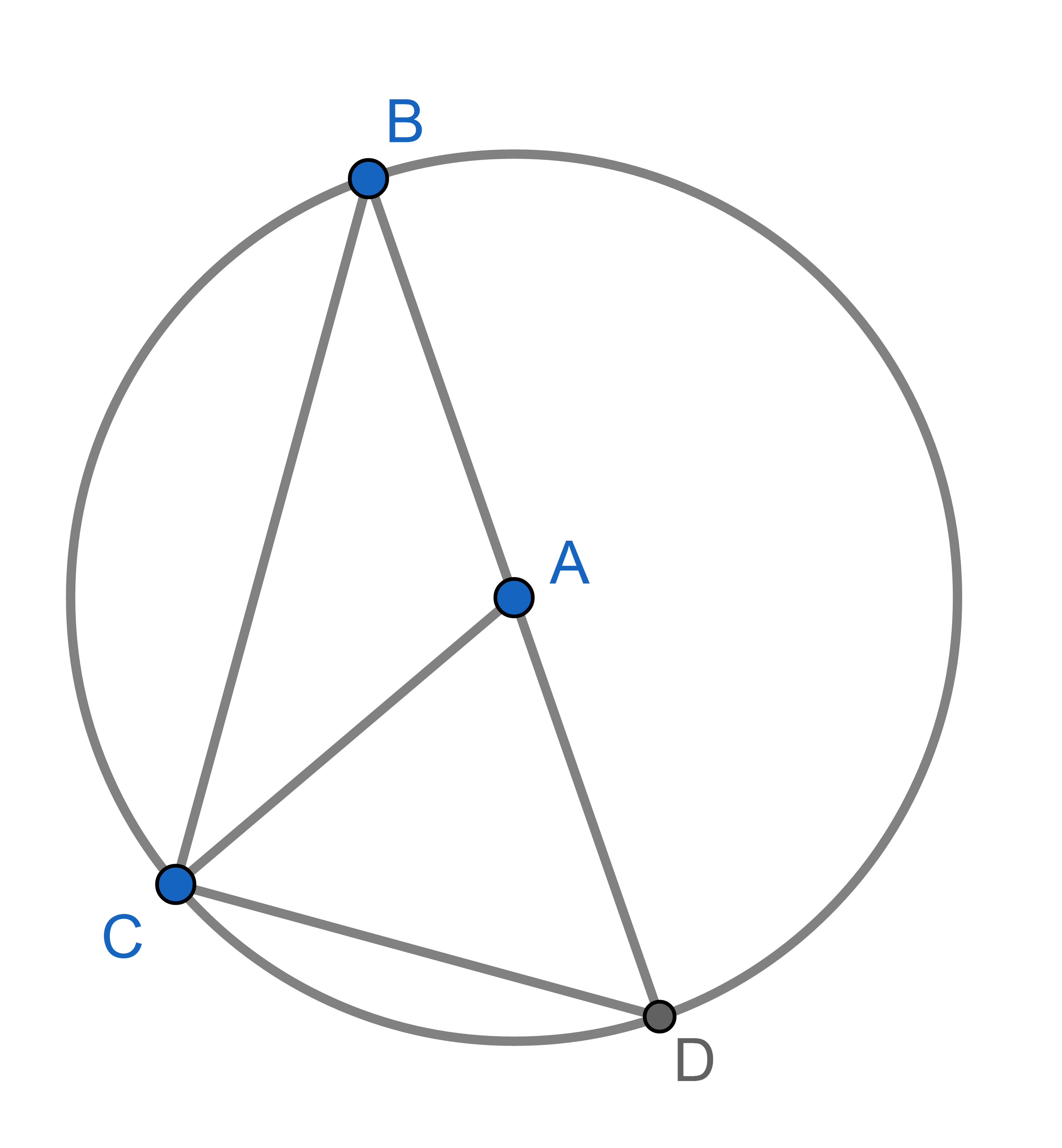
Point \(A\) is the centre of a circle and points \(B,C,D\) lie on that circle. The segment \(BD\) is a diameter of the circle. Show that \(\angle CAD = 2 \angle CBD\). This is a special case of the inscribed angle theorem.