Problems

Let \(X\) be a finite set, and let \(\mathcal{P}X\) be the power set of \(X\) - that is, the set of subsets of \(X\). For subsets \(A\) and \(B\) of \(X\), define \(A*B\) as the symmetric difference of \(A\) and \(B\) - that is, those elements that are in either \(A\) or \(B\), but not both. In formal set theory notation, this is \(A*B=(A\cup B)\backslash(A\cap B)\).

Prove that \((\mathcal{P}X,*)\) forms a group.

The lengths of three sides of a right-angled triangle are all integers.

Show that one of them is divisible by \(5\).

You have a row of coins and you can perform these three operations as many times as you like:

1. Remove three adjacent heads

2. Remove two adjacent tails

3. If there’s a tail followed by a heads, then turn the tail over and put a new tail after both heads

You apply these operations until you can’t make any more moves. Show that you will always get the same configuration at the end, no matter the order.

Let \(a\) be a positive integer, and let \(p\) be a prime number. Prove that \(a^p - a\) is a multiple of \(p\).

We ‘typically’ use the formula \(\frac{1}{2}bh\) for the area of a triangle, where \(b\) is the length of the base, and \(h\) is the perpendicular height. Here’s another one, called Heron’s formula.

Call the sides of the triangle \(a\), \(b\) and \(c\). The perimeter is \(a+b+c\). We call half of this the semiperimeter, \(s=\frac{a+b+c}{2}\). Then the area of this triangle is \[\sqrt{s(s-a)(s-b)(s-c)}.\] Prove this formula is correct.

The perimeter of the triangle \(\triangle ABC\) is \(10\). Let \(D,E,F\) be the midpoints of the segments \(AB,BC,AC\) respectively. What is the perimeter of \(\triangle DEF\)?

Let \(\triangle ABC\) be a triangle and \(D\) be a point on the edge \(BC\) so that the segment \(AD\) bisects the angle \(\angle BAC\). Show that \(\frac{|AB|}{|BD|}=\frac{|AC|}{|CD|}\).

The Great Pyramid of Giza is the largest pyramid in Egypt. For the purposes of this problem, assume that it’s a perfect square-based pyramid, with perpendicular height \(140\)m and the square has side length \(230\)m.

What is its volume in cubic metres?

The volume of a pyramid is \(\frac{1}{3}Bh\), where \(B\) is the area of the base and \(h\) is the perpendicular height. What’s the volume of a regular tetrahedron with side length \(1\)?

A regular octahedron is a solid with eight faces, all of which are equilateral triangles. It can be formed by placing together two square based pyramids at their bases.

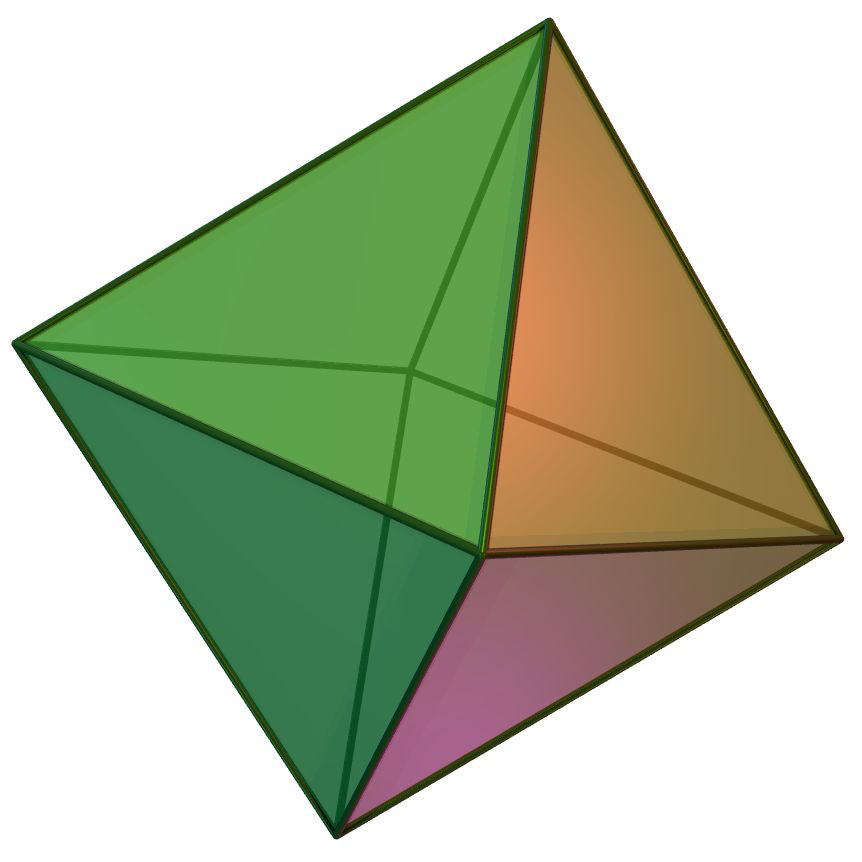
What is the volume of an octahedron with side length \(1\)?