Problems

Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a semicircle

In his twelfth year on the island Robinson Crusoe managed to tame a wolf, and used him as a guard dog for his goat. He used to tie the wolf with ropes to pegs and other ropes in such a way that there was always a safe place for the goat to escape. Subsequently, he studied the shapes the goat was grazing on the ground.
Draw a picture how Robinson used to tie the goat and the wolf in order for the goat to graze the grass in the shape of a ring

Think of other shapes Robinson’s goat can graze without a wolf, or with a wolf tied nearby. What if Robinson managed to tame several wolves and used them as guard dogs? Can two tied wolves keep an untied goat in a triangle? Can you think of other shapes you can create with Robinson’s goat and wolves?

A rectangle is made up from six squares. Find side length of the largest square if side length of the smallest square is 1.

This shape below is made up from squares.

Find side length of the bottom square if side length of the smallest square is equal to 1.

You are given a convex quadrilateral. Is it always possible to cut out a parallelogram out of the quadrilateral such that three vertices of the new parallelogram are the vertices of the old quadrilateral?

The edges of a cube are assigned with integer values. For each vertex we look at the numbers corresponding to the three edges coming from this vertex and add them up. In case we get 8 equal results we call such cube “cute”. Are there any “cute” cubes with the following numbers corresponding to the edges:

(a) \(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12\);

(b) \(-6, -5, -4, -3, -2, -1, 1, 2, 3, 4, 5, 6\)?

The area of a rectangle is 1 cm\(^2\). Can its perimeter be greater than 1 km?

a) There are six points on a plane. No matter which five points you choose you can cross them with two lines but one cannot find two lines which cross all six of them. Does such configuration exist?

(b) One extremely successful businesswoman is planning to build a garden in her country house. She wants to have 10 garden beds and several lanes built. She requested her architect to organize the garden in such a way that for every nine beds there are three lanes passing by them (for each garden bed out of these nine beds there is a lane among the three lanes which passes by it). On top of that she demanded that there should not be three lanes which pass by all 10 garden beds. How can the poor architect satisfy this requirement? All lanes have to be straight.

(c) A neighbour of the businesswoman is inspired by her exotic demands. He decides to surpass her on this field. The neighbour plans to build 55 garden beds. They have to be joined by several lanes in such a way that for every 54 garden beds you can find nine lanes crossing them (for each garden bed out of these 54 beds there is a lane among the nine lanes which crosses this bed). Can you help the colleague of the architect? Again all the lanes have to be straight.

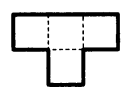
Two figures are said to be similar if all their corresponding sides are congruent and corresponding angles are equal. By using several copies of the figure below construct a bigger figure that is similar.