Problems

Let \(A\), \(B\), \(C\), \(D\), \(E\) be five different points on the circumference of a circle in that (cyclic) order. Let \(F\) be the intersection of chords \(BD\) and \(CE\). Show that if \(AB=AE=AF\) then lines \(AF\) and \(CD\) are perpendicular.

Let \(u\) and \(v\) be two positive integers, with \(u>v\). Prove that a triangle with side lengths \(u^2-v^2\), \(2uv\) and \(u^2+v^2\) is right-angled.

We call a triple of natural numbers (also known as positive integers) \((a,b,c)\) satisfying \(a^2+b^2=c^2\) a Pythagorean triple. If, further, \(a\), \(b\) and \(c\) are relatively prime, then we say that \((a,b,c)\) is a primitive Pythagorean triple.

Show that every primitive Pythagorean triple can be written in the form \((u^2-v^2,2uv,u^2+v^2)\) for some coprime positive integers \(u>v\).

The lengths of three sides of a right-angled triangle are all integers.

Show that one of them is divisible by \(5\).

The perimeter of the triangle \(\triangle ABC\) is \(10\). Let \(D,E,F\) be the midpoints of the segments \(AB,BC,AC\) respectively. What is the perimeter of \(\triangle DEF\)?

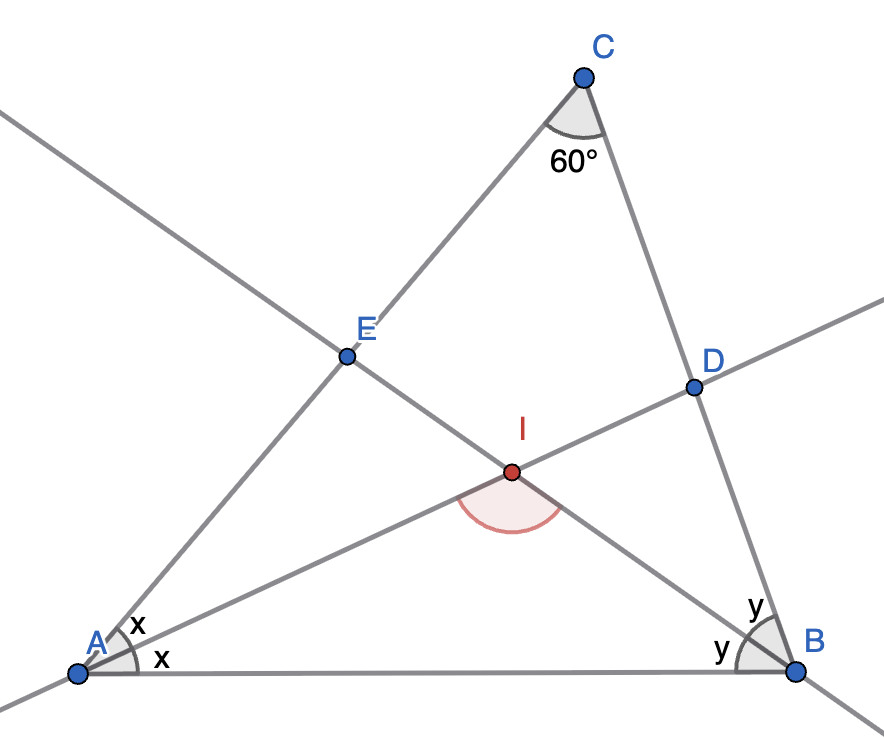
In the triangle \(\triangle ABC\), the angle \(\angle ACB=60^{\circ}\), marked at the top. The angle bisectors \(AD\) and \(BE\) intersect at the point \(I\).

Find the angle \(\angle AIB\), marked in red.

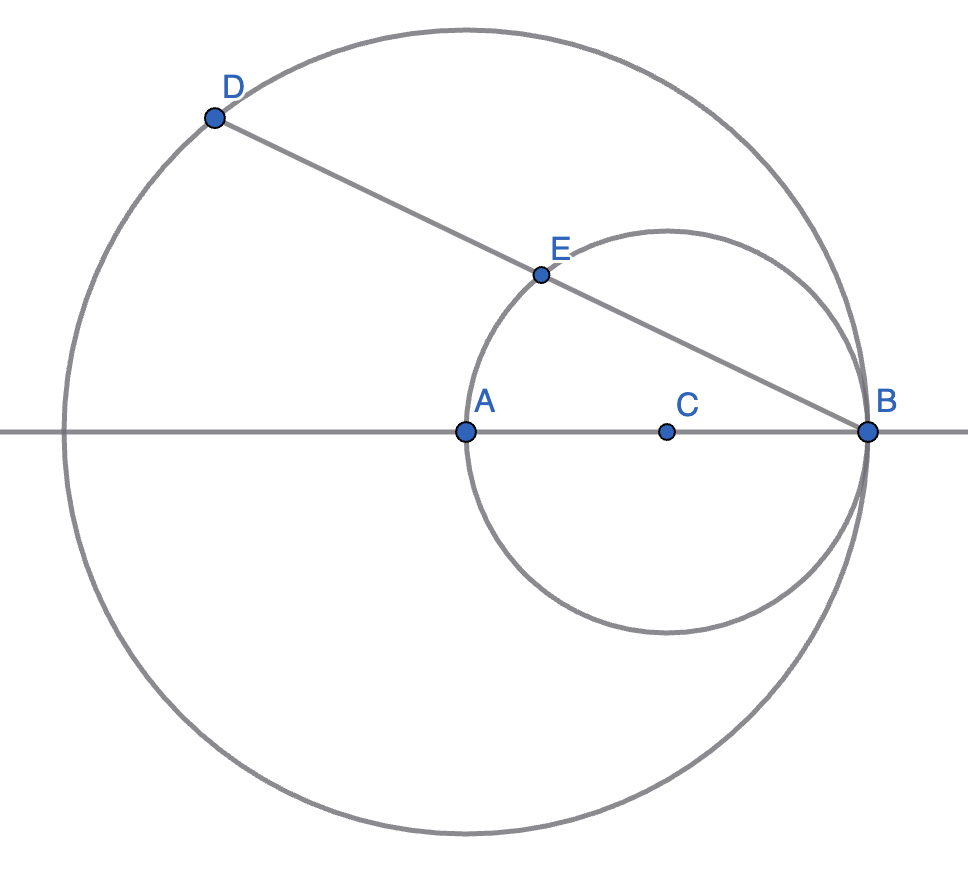
A circle with centre \(A\) has the point \(B\) on its circumference. A smaller circle is drawn inside this with \(AB\) as a diameter and \(C\) as its centre. A point \(D\) (which is not \(B\)) is chosen on the circumference of the bigger circle, and the line \(BD\) is drawn. \(E\) is the point where the line \(BD\) intersects the smaller circle.

Show that \(|BE|=|DE|\).