Problems

Sometimes it is hard to rigorously formulate an intuitively correct reasoning. We might not know the proper words, the proper language, we might not have the right tools. Maths problems are not an exception. When we start learning to solve them, we know nothing about possible mathematical approaches and mathematical models. Today you will learn a very useful way to visualise information: you will learn how to represent information as a graph.

A graph is a finite set of points, some of which are connected with line segments. The points of a graph are called vertices. The line segments are called edges.

In a mathematical problem, one may use vertices of a graph to represent objects in the problem, i.e. people, cities, airports, etc, and edges of the graph represent relations between the objects such as mutual friendship, railways between cities, plane routes, etc. As you will see in the examples below, representing the initial problem as a graph can considerably simplify the solution.

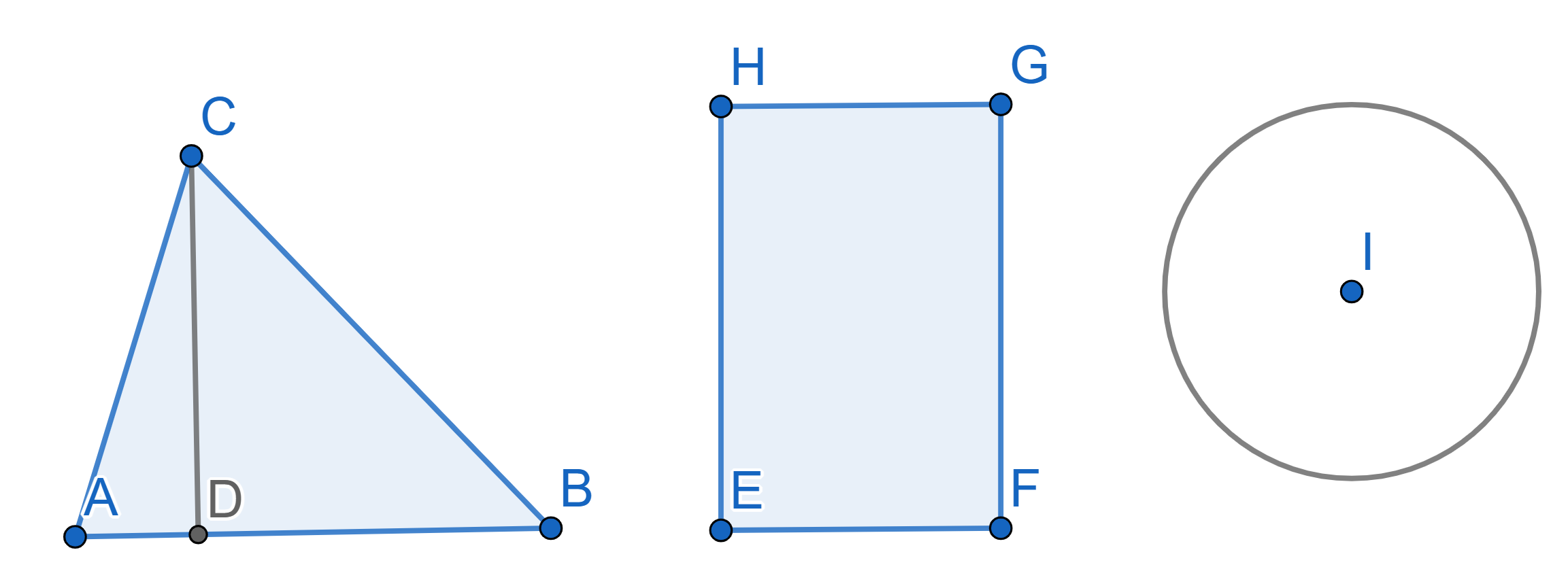
Today we will solve some problems about finding areas of geometric figures. You only need to know how to calculate the area of a rectangle, a triangle and a circle to be able to solve every problem in this set. Here is a brief description of the area formula for each shape.

We start with rectangles because they are easy. In the picture below, one way to find the area of the rectangle is to multiple the length of the side \(AB\) by the length of the side \(AD\).

Next we consider the area of a triangle. In general, the area of a triangle is given by \(\frac{1}{2}bh\), where \(b\) is the length of a chosen base and \(h\) is the height (the length of the altitude corresponding to that base). Finding a base and a corresponding altitude is usually straightforward. However, it can be a bit tricky if the altitude lies outside the triangle. See the picture below for one such case. The segment \(AB\) is the base and \(CD\) is the altitude.

At last, we come to the area of a circle. If a circle has radius \(r\), its area is \(\pi r^2\). A fully rigorous proof requires calculus! The number \(\pi\) is approximately 3.14159 to five decimal points.

Prime numbers are like atoms that build every integer number. That is, a prime decomposition of a number is unique and then we can use it to find the number’s factors. Today we will explore this idea a bit more.

We will introduce a couple of new terms. First, a common divisor of two numbers is simply a number that both of these numbers can be divided by. Two numbers which have no common divisors (except from 1) are called relatively prime. We can establish if two numbers are relatively prime by looking at their prime factorizations - if they share no common primes, then they cannot share a common divisor!

Out of all the common divisors two numbers have, one must be the largest. This is an important number and is called the Greatest Common Divisor (GCD). You can find it by looking at the prime factorizations of the two numbers. For every prime number appearing in both factorizations, we take the smaller power. Then we multiply all our choices together. If we divide both numbers by their GCD, the resulting numbers will have no common divisors left and so will be relatively prime.

Similar to the notion of a common divisor is the one of common multiple. It is simply a number that is divisible by both numbers. Among the common multiples, one must be the smallest – this is called the Least Common Multiple (LCM). Again, the LCM can be found by looking at the prime factorizations of the two numbers. For every prime number appearing in any of the two factorizations, we take the larger power. Then we multiply all our choices together.

A remainder is the number that is “left over" from division. Even if a number is not divisible by another number fully, we can still divide, but leaving a remainder. The remainder is less than the number we’re dividing by. For example, a remainder of \(44\) in division by \(7\) is \(2\), because \(44 = 6 \times 7 + 2\).

More generally, given any integer \(n\) and positive integer \(k\), we can always write \(n=qk+r\), where \(0\leq r<k\). We say that \(k\) goes into \(n\) \(q\) times, and a little bit (\(r\)) is left. If that little bit was larger than \(k\), it could “go into" \(n\) once more. This means we can always enforce the condition \(0\leq r<k\) on the remainder \(r\).

The general rule is that the remainder of a sum, difference or a product of two remainders is equal to the remainder of a sum, difference or a product of the original numbers. What that means is if we want to find a remainder of a product of two numbers, we need to look at the individual remainders, multiply them, and then take a remainder.

For example, \(10\) leaves the remainder \(3\) when divided by \(7\) and \(11\) leaves the remainder \(4\) when divided by \(7\). The product \(10\times11=110\) has the same remainder as the product of the individual remainders. We first multiply \(3\times4=12\) and then calculate the remainder upon division by \(7\), which is \(5\) because \(12=7+5\). That means that \(110\) gives a remainder of \(5\) when divided by \(7\). We can verify the result by calculating the remainder without simplifying first: \(110=15\times7+5\).

Here is a useful notation when discussing problems involving remainders and divisibility although it is not necessary for this problem sheet. Take two integers \(a\) and \(b\). If they differ by a multiple of a positive integer \(k\), then we write \(a \equiv b \pmod{k}\). For example, since \(24 - 10 = 2 \times 7\), we can express this fact by \(10 \equiv 24 \pmod{7}\). We say that 10 and 24 are congruent modulo 7.

Using this new notation, we can easily express the rules for remainders. Let \(a \equiv b \pmod{k}\) and \(c \equiv d \pmod{k}\). Then we have \(a + c \equiv b + d \pmod{k}\) and \(a \times c \equiv b \times d \pmod{k}\). As an example, again consider the calculation of the remainder of \(10 \times 11\) when divided by 7. We have \(10 \times 11 \equiv 3 \times 4 \equiv 12 \equiv 5 \pmod{7}\).

We make one last observation, which shows the utility of remainder when discussing divisibility. Saying that a number \(a\) is divisible by a number \(k\) is the same as saying the remainder of \(a\) when divided by \(k\) is 0. In congruence notation, the latter condition is \(a \equiv 0 \pmod{k}\).

Let’s have a look at some examples with remainders:

Today we will discover some ideas related to non-isosceles triangles. This restriction comes from the fact that in isosceles triangles, a median and a height coincide.

Welcome back! The topic of this sheet is: dissections and gluings. This means that we will take shapes, break them apart, and put the pieces back together to form interesting objects. Sometimes, we will also “glue" objects together and see how they can be used to construct other shapes. Let’s see a few simple examples:

Today we will learn a really useful strategy for solving a certain kind of problems. This strategy is called the invariance principle, and after working through this sheet you’ll be able to recognise easily when we need to use an invariant to solve a problem. This strategy is applicable to kinds of problems where some task is repeatedly performed, and we wish to see if it is possible to transform our “initial state" into some given “final state". The key is to ask yourself:

The topic of this problem sheet will be polynomials. Before we dive into the examples, let’s recap a few key concepts.

A polynomial in \(x\) is an expression formed by adding or subtracting monomials, which are terms of the form \(a x^n\), where \(a\) is a number called a coefficient, and \(n\) is a whole number (non-negative integer). Here, \(x\) is a variable that may represent a number. The degree of a polynomial \(f\), written as \(\deg(f)\) is the highest power of \(x\) appearing in the polynomial. For example: \(\deg(x^3+x^2+x)=3\).

We can perform several familiar operations on polynomials, which you may have seen before:

• Addition and subtraction: We add or subtract polynomials by looking at each power of \(x\) and adding or subtracting the corresponding coefficients. For example, if \[f(x) = x^4 + 3x - 1 \quad \text{and} \quad g(x) = x^3 + 2x + 5,\] then \(f(x) - g(x) = x^4 - x^3 + x - 6\).

• Multiplication: We use the distributive property, which means that every term in the first polynomial is multiplied by every term in the second polynomial. For example, if \[f(x) = x^2 + x + 1 \quad \text{and} \quad g(x) = x - 1,\] then \(f(x) g(x) = (x^2 + x + 1)(x - 1) = x^3 + x^2 + x - x^2 - x - 1 = x^3 - 1.\)

Let’s now present the examples. They have some very important techniques, so read them carefully before attempting the problems.

Today we will solve some problems using algebraic tricks, mostly related to turning a sum into a product or using an identity involving squares.
The ones particularly useful are: \((a+b)^2 = a^2 +b^2 +2ab\), \((a-b)^2 = a^2 +b^2 -2ab\) and \((a-b) \times (a+b) = a^2 -b^2\). While we are at squares, it is also worth noting that any square of a real number is never a negative number.

Certain geometric objects nicely blend when they happen to be together in a problem. One possible example of such a pair of objects is a circle and an inscribed angle.
We will be using the following statements in the examples and problems:
1. The supplementary angles (angles “hugging" a straight line) add up to \(180^{\circ}\).
2. The sum of all internal angles of a triangle is also \(180^{\circ}\).

3. Two triangles are said to be “congruent" if ALL their corresponding sides and angles are equal.
We recommend solving the problems in this sheet in the order of appearance, as some problems use statements from previous problems as a step in the solution. Specifically, the inscribed angle theorem (problem 2) is required to solve every other problem that comes after it.