Problems

In a lot of geometric problems the main idea is to find congruent figures. We call two polygons congruent if all their corresponding sides and angles are equal. Triangles are the easiest sort of polygons to deal with. Assume we are given two triangles \(ABC\) and \(A_1B_1C_1\) and we need to check whether they are congruent or not, some rules that help are:

• If all three corresponding sides of the triangles are equal, then the triangles are congruent.

• If, in the given triangles \(ABC\) and \(A_1B_1C_1\), two corresponding sides \(AB=A_1B_1\), \(AC=A_1C_1\) and the angles between them \(\angle BAC = \angle B_1A_1C_1\) are equal, then the triangles are congruent.

• If the sides \(AB=A_1B_1\) and pairs of the corresponding angles next to them \(\angle CAB = \angle C_1A_1B_1\) and \(\angle CBA = \angle C_1B_1A_1\) are equal, then the triangles are congruent.

At a previous geometry lesson we have derived these rules from the axioms of Euclidean geometry, so now we can just use them.

Today we will be solving problems using the pigeonhole principle. What is it? Simply put, we are asked to place pigeons in pigeonholes, but the number of pigeons is larger than the number of pigeonholes. No matter how we try to do that, at least one pigeonhole will have to contain at least 2 pigeons. By ”pigeonholes” we can mean any containers and by ”pigeons” we mean any items, which are placed in these containers. This is a simple observation, but it is helpful in solving some very difficult problems. Some of these problems might seem obvious or intuitively true. Pigeonhole principle is a useful way of formalising things that seem intuitive but can be difficult to describe mathematically.

There is also a more general version of the pigeonhole principle, where the number of pigeons is more than \(k\) times larger than the number of pigeonholes. Then, by the same logic, there will be one pigeonhole containing \(k+1\) pigeons or more.

A formal way to prove the pigeonhole principle is by contradiction - imagine what would happen if each pigeonhole contained only one pigeon? Well, the total number of pigeons could not be larger than the number of pigeonholes! What if each pigeonhole had \(k\) pigeons or fewer? The total number of pigeons could be \(k\) times larger than the number of pigeonholes, but not greater than that.

A graph is a finite set of points, some of which are connected with line segments. The points of a graph are called vertices. The line segments are called edges. In this problem set we only consider graphs in which every pair of vertices is connected with one or zero edges.

In a mathematical problem, one may use vertices of a graph to represent objects in the problem, i.e. people, cities, airports, and edges of the graph represent relations between the objects such as mutual friendship, railways between cities, plane routes. As you will see in the examples below, representing the initial problem as a graph can considerably simplify the solution.

Imagine you are a manager of a very special hotel, a hotel with an infinite number of rooms, where each room has a natural number on the door \(1,2,3,4,...\). Only one guest can stay in each room and in most cases the hotel will be initially full with no vacant rooms left.
You will have to deal with unusual situations that may occur.

Today we will draw lots of pictures.

The subject is Topology. It is often called “rubber-sheet geometry" because while it is the study of shapes, topologists typically do not pay too much attention to rigid notions like angle and lengths. We have much more flexibility in topology. Some common words describing the operations here might include “gluing", “stretching", “twisting" and “inflating".

Although we will not define continuity, it is a more or less intuitive idea. Topological operations should be continuous. If you have a line segment, no amount of stretching, twisting or bending can make it into two disconnected segments.

In this sheet, we will look at basic counting problems. The fundamental principle is quite simple. If you have two independent choices to make, then the number of options for making both choices is calculated by multiplying the number of options for each choice.

An issue we frequently run into is that of overcounting. This means we count the same thing more than once. In the examples and problems today, you will see various ideas that we can use to correct for overcounting, or for avoiding it.

From the examples above, we see that we often need to pick \(k\) objects from \(n\) objects where the order of the \(k\) objects is ignored. The number of ways to pick them is notated with the special symbol \(\binom{n}{k}\), pronounced “\(n\) choose \(k\)". Following a similar line of reasoning as the examples, we can write down a general formula:

\[\binom{n}{k} = \frac{n\times (n-1) \times \dots (n-k+1)}{k\times (k-1) \times \dots 1} = \frac{n!}{k!(n-k)!}.\]

\(n!\) is a shorthand for \(n\times (n-1)\times \dots \times 1\), pronounced “\(n\) factorial". This is another useful expression and allows us to write down many formulas succinctly.

Today we will solve some geometric problems using the triangle inequality. This is an inequality between the lengths of the sides of any triangle, or between the distances of any three points.

The shortest path between any two points \(A\) and \(B\) is a straight segment - every other path is longer. In particular, a path through another point, \(C\), is equal or longer. \[AC + BC \ge AB\] The triangle inequality says that the sum of lengths of any two sides of a triangle is always larger than the length of the third side. The inequality only becomes an equality if \(ABC\) is not actually a triangle and the point \(C\) lies on the segment from \(A\) to \(B\).

Even though it is a simple idea, it can be a really helpful tool in problem solving.

Today we will solve some logic problems. This time, we are visiting a strange planet. This planet is inhabited by two kinds of aliens, Cricks and Goops. The physical differences between them are not enough for a human being to distinguish them, but they have another remarkable feature. They can only ask questions. Cricks can only ask questions whose answer is yes, while Goops can only ask questions whose answer is no.

A set is a collection of objects of any specified kind, the objects are called elements or members, the objects in one set cannot repeat, namely \(\{1,2,3\}\) and \(\{1,2,2,2,3\}\) are identical sets. We denote a set by a capital letter \(A\), or \(B\) and write \(x\in A\) if \(x\) is an element of \(A\), and \(x\notin A\) if it is not. The notation \(A=\{a,b,c,...\}\) means that the set \(A\) consists of the elements \(a,b,c,...\). The empty or void set, \(\emptyset\), has no elements. If all elements of \(A\) are also in \(B\), then we call \(A\) a subset of \(B\) and we write \(A\subseteq B\). It is an axiom that the sets \(A\) and \(B\) are equal \(A=B\) if they have the same elements. Namely, \(A\) is a subset of \(B\) and \(B\) is a subset of \(A\) at the same time.
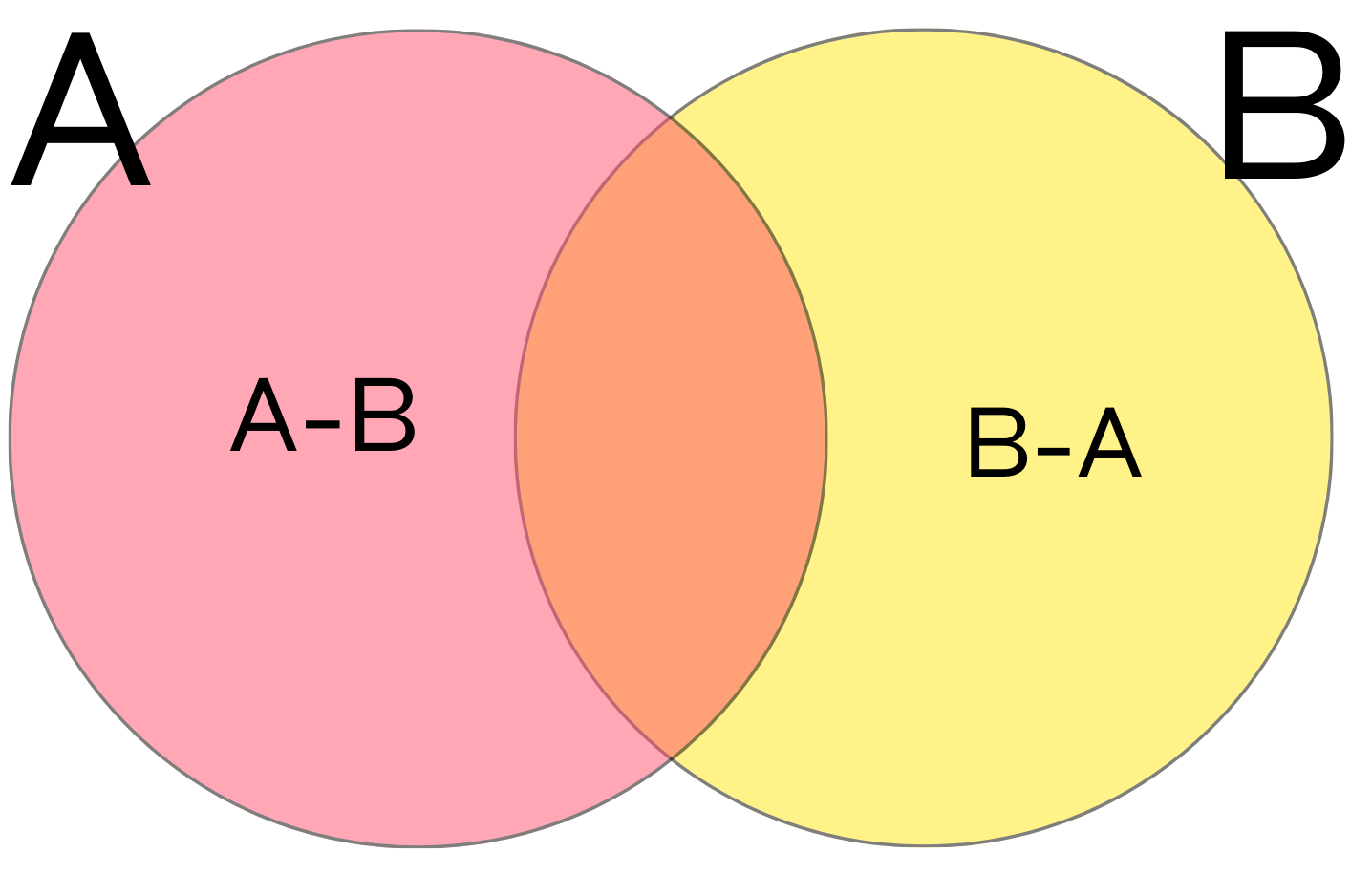
For any sets \(A\) and \(B\), we define their union \(A\cup B\), intersection \(A\cap B\), and the difference \(A-B\) as follows:

• the union \(A\cup B\) is the set of all elements that belong to \(A\) or \(B\);

• the intersection \(A\cap B\) is the set of elements that belong to both \(A\) and \(B\);

• the difference \(A-B\) consists of those \(x \in A\) that are do not belong to \(B\).

Sometimes it is useful to draw sets as Venn diagrams, on the diagram below the pink circle represents the set \(A\), the yellow circle represents the set \(B\), the orange part is the intersection \(A\cap B\), the pink part is \(A-B\), the yellow part is \(B-A\), and the whole picture is the union \(A\cup B\).